Двойственность в линейном программировании, страница 11

Полученный ответ будет иметь смысл лишь в том случае, если значения всех переменных будут неотрицательны (т.е. последняя таблица будет допустимой). Поэтому необходимо проверить знак базисных переменных x₁,  x₅,  х₂,  x₇,  х₄; т.е. определить, при каких изменениях свободных членов они будут неотрицательны. Составим систему неравенств:

0,011 - 0,011_Db₃ + _Db₅ ³ 0

0,489 + 0,011_Db₃ ³ 0

0,711 - _Db₁ - 4,211_Db₃ + 380_Db₅ ³ 0

1,289 + _Db₂ + 4,211_Db₃ - 380_Db₅ ³ 0

15,222 - 0,022_Db₃ + _Db₄ ³ 0

Чтобы решить эту систему, вначале предположим, что меняется только минимальное содержание кальция, т.е. первый свободный член. Тогда _Db₂  = _Db₃  = _Db₄ = _Db₅ = 0, и система примет вид:

0,011 ³ 0

0,489 ³ 0

0,711 - _Db₁ ³ 0

1,289 ³ 0

15,222 ³ 0

Отсюда _Db₁ £ 0,711. В первоначальном варианте исходных данных b₁ =
= 4. Следовательно, двойственная оценка y₁ = 0 будет устойчивой лишь при норме минимального содержания кальция от любого значения до 4,711 г (4 +
+ 0,711 = 4,711). Можно сказать, что оптимальная стоимость корма не изменится (изменится на 0 руб.), если потребуется, чтобы в корме содержалось, например, не менее 4,5 г кальция, или не менее 4,7 г кальция, или не менее 2 г кальция, или будет допускаться, чтобы вообще не содержалось кальция. Если эта норма будет повышена, например, до 5 г кальция (5,5 г, 4,8 г, 100 г и т.д.), то неизвестно, на сколько изменится оптимум задачи.

Теперь предположим, что меняется только максимальное содержание кальция, т.е. второй свободный член. Тогда _Db₁  = _Db₃  = _Db₄ = _Db₅ = 0, и система примет вид:

0,011 ³ 0

0,489 ³ 0

0,711 ³ 0

1,289 + _Db₂ ³ 0

15,222 ³ 0

Отсюда _Db₂ ³ -1,289. Следовательно, двойственная оценка y₂ = 0 будет устойчивой при норме максимального содержания кальция от 4,711 г
(6 - 1,289 = 4,711) до любого значения. Можно сказать, что оптимальная стоимость корма не изменится, если потребуется, чтобы в корме содержалось, например, не более 4,8 г кальция, или не более 10 г кальция, или будет допускаться, чтобы кальция было сколь угодно много. Если эта норма будет снижена, например, до 4,5 г кальция (4,7 г, 1 г, 0 г и т.д.), то неизвестно, на сколько изменится оптимум задачи.

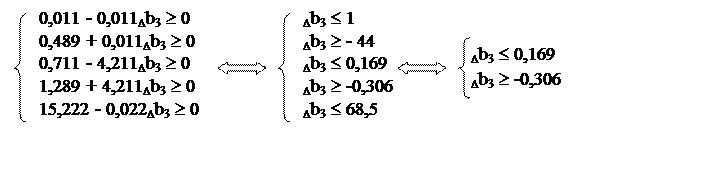Если предположить, что меняется только минимальное содержание белка, то _Db₁  = _Db₂  = _Db₄ = _Db₅ = 0, и система примет вид*:

Следовательно, двойственная оценка y₃ = 0,122 будет устойчивой при норме минимального содержания белка от 43,694 г до 44,169 г. Можно сказать, что если потребуется, чтобы в корме содержалось, например, не менее 43,7 г белка, то оптимальная стоимость рациона уменьшится на 0,122*(44 – 43,7) = 0,122*0,3 = 0,0366 (руб.).  Если граничное содержание белка составит 44,1 г, то эта стоимость возрастет на 0,122*(44,1 – 44) = 0,0122 (руб.); и т.п. Но если граничное содержание белка составит, например, 43 г, или 10 г, или 44,2 г, или 100 г и т.п., то неизвестно, на сколько изменится оптимум задачи, поскольку при этом исходные данные выйдут за интервал устойчивости двойственных оценок.

При изменении нормы содержания клетчатки _Db₁  = _Db₂  = _Db₃ = _Db₅ = 0, и система примет вид:

0,011 ³ 0

0,489 ³ 0

0,711 ³ 0

1,289 ³ 0

15,222 + _Db₄ ³ 0

Отсюда _Db₄ ³ -15,222. Следовательно, двойственная оценка y₄ = 0 будет устойчивой при норме содержания клетчатки от 9,778 г до любого значения.

И, наконец, при изменении заданной массы корма _Db₁  = _Db₂  = _Db₃ =
= _Db₄ = 0, и система примет вид:

0,011 + _Db₅ ³ 0

0,489 ³ 0

0,711 + 380_Db₅ ³ 0

1,289 - 380_Db₅ ³ 0

15,222 ³ 0

Отсюда -0,003 £ _Db₅ £ 0,002. Следовательно, двойственная оценка y₅ =
= 4 будет устойчивой при массе рациона от 0,497 г до 0,502 г.