2 Геометрическая интерпретация и графический способ решения задачи линейного программирования. 24
2.1 Решение задачи производственного планирования. 24
2.2 Геометрическая интерпретация задачи линейного программирования. 30
2.2.1 Построение области допустимых планов. 31
2.2.2 Нахождение оптимального плана. 36
2.2.3 Разрешимость задачи линейного программирования. 36
2.2.4 Множественное решение. 38
2.3. Пример решения задачи графическим способом с помощью Excel 40
2.4 Вопросы и упражнения. 48
Решим задачу производственного планирования, построенную в разделе 1.1. Для этого введем на плоскости систему координат, обозначив горизонтальную ось х1, а вертикальную – х2 (рисунок 2). Это означает, что по горизонтали мы будем откладывать производство карамели «Снежинка» (т), а по вертикали – производство карамели «Яблочная» (т). Теперь любая точка на плоскости представляет собой план задачи.
Выделим на рисунке 2 любые три точки. Например, точка с координатами (500; 1500) представляет собой следующий план: кондитерская фабрика выпускает 500 т карамели «Снежинка» и 1500 т карамели «Яблочная». Точка (1500; 0) означает, что фабрика выпускает 1500 т «Снежинки», а «Яблочную» не выпускает вообще. Точка О (начало координат) означает, что фабрика вообще не выпускает карамель. И т.п.
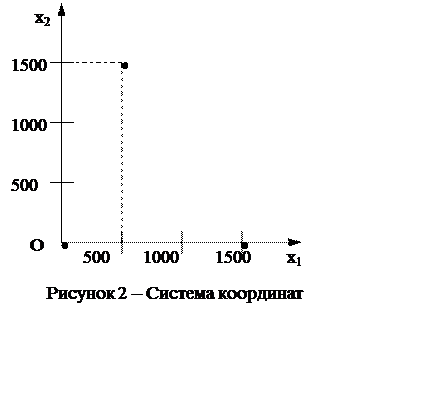
Итак, вся плоскость – планы задачи. Выберем из них допустимые планы, т.е. такие, которые фабрика сможет осуществить.
Поскольку обе переменные в этой задаче должны быть неотрицательны, будем рассматривать только неотрицательную координатную четверть (все, что левее оси ординат или ниже оси абсцисс, нас не интересует).
Теперь рассмотрим остальные ограничения. Начнем с ограничения по запасам сахарного песка: 0,8х1 + 0,5х2 £ 800. Представим себе, что фабрика обязательно должна израсходовать все 800 т сахара (не больше и не меньше). Тогда ограничение примет вид уравнения: 0,8х1 + 0,5х2 = 800*. На плоскости это уравнение прямой. Построим эту прямую (рисунок 3). При подстановке координат любой точки на этой прямой в левую часть уравнения, получается ровно 800 (и все такие точки лежат на этой прямой). Значит, при осуществление любого плана выпуска карамели, лежащего на этой прямой, будет израсходовано ровно 800 т сахара.
Теперь «вспомним» о том, что на самом деле это ограничение – неравенство (т.е. можно израсходовать меньше 800 т сахарного песка). Следовательно, нас интересует не сама прямая, а полуплоскость. Любая прямая делит плоскость на 2 полуплоскости. Чтобы выбрать из них нужную, возьмем в любой полуплоскости произвольную точку и подставим ее в неравенство. Если оно окажется истинным, то полуплоскость выбрана верно, а если нет, то надо выбрать другую. Здесь удобно взять точку (0; 0). При подстановке получаем 0,8*0 + 0,5*0 = 0 £ 800. Неравенство истинно (в самом деле, запасы сахара явно позволяют не выпускать карамель, - ведь если фабрика ее не выпускает, то и сахарный песок не расходуется вообще). Следовательно, допустимые планы лежат в той полуплоскости относительно прямой, в которой лежит (0; 0). Покажем эту полуплоскость маленькой стрелкой рядом с прямой (см. рисунок 3).

Теперь известно, что допустимые планы задачи могут находиться только в треугольнике, заштрихованном на рисунке 4 (это пересечение, т.е. общая часть, неотрицательной координатной четверти и выбранной полуплоскости).
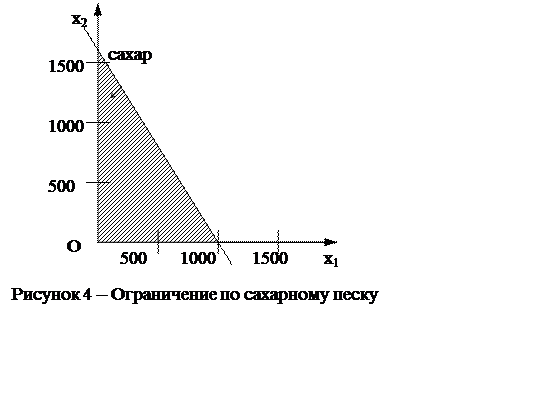
Однако в задаче есть еще два ограничения – по запасам патоки и фруктового пюре. Построим аналогично ограничение по запасам патоки: 0,2х1 + 0,4х2 £ 600 (рисунок 5).
В данном случае, добавив новое ограничение, мы «отсекли» часть треугольника. Теперь допустимые планы могут находиться только в четырехугольнике, заштрихованном на рисунке 5. Только в этом четырехугольнике находятся все такие планы производства карамели, для осуществления которых фабрике хватит и сахарного песка, и патоки (и обе переменные при этом неотрицательны).
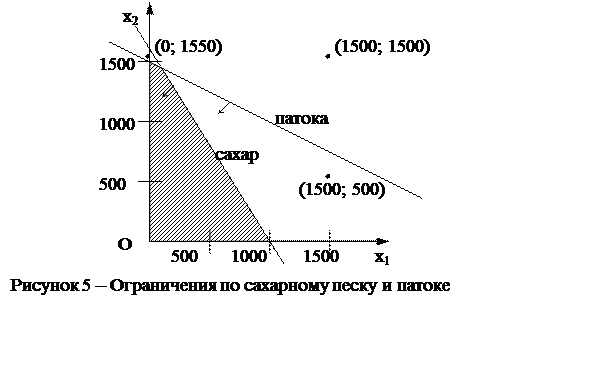
Все остальные планы будут недопустимыми. Например, для осуществления плана (0; 1550) не хватит патоки (хотя сахарного песка хватит). Для осуществления плана (1500; 500) хватит сахарного песка, но не хватит патоки (он тоже недопустимый). Для плана (1500; 1500) не хватит ни одного из этих ресурсов. Три плана, рассмотренные в качестве примера, на рисунке 5 выделены.
Осталось рассмотреть еще одно ограничение: по запасам фруктового пюре: 0,01х1 + 0,1х2 £ 120. После того, как оно изображено на графике, ОДП задачи примет вид четырехугольника, представленного на рисунке 6.
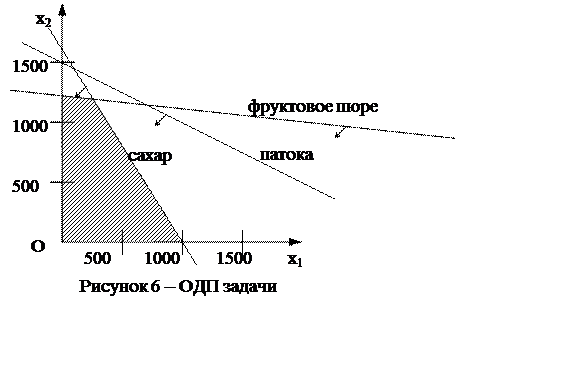
Теперь на графике отражены все ограничения. Каждому из них соответствует прямая и полуплоскость (в том числе и ограничениям неотрицательности: для ограничения х2 ³ 0 это ось абсцисс, а для х1 ³ 0 – ось ординат с соответствующими полуплоскостями сверху и справа от осей).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.