Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 4

В этой области существуют планы со сколь угодно большими значениями обеих координат – и х₁, и х₂.

Предположим, например, что в задаче поставлено единственное ограничение (помимо ограничений неотрицательности) – выпустить ровно 1000 т карамели «Снежинка» (х₁ = 1000). Тогда ОДП задачи будет представлять собой луч (полупрямую), представленный на рисунке 14 (ОДП выделена более жирной линией). Эта ОДП тоже не ограничена, так как одна координата – х₂ - может принимать сколь угодно большие значения.

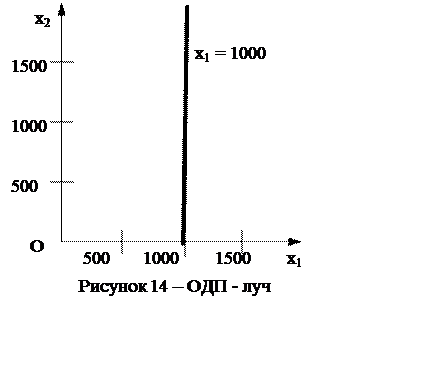
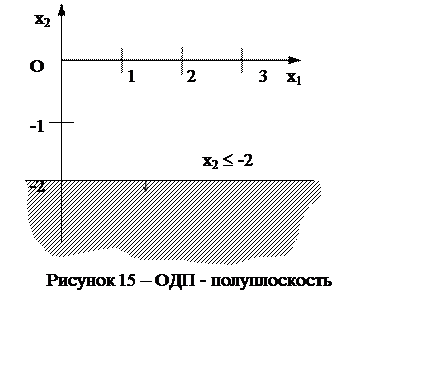
Чтобы привести пример ОДП в виде полуплоскости, рассмотрим задачу с единственным ограничением: х₂ £ -2. Такая ОДП заштрихована на рисунке 15. Она тоже неограниченная: здесь обе координаты могут принимать бесконечно большие по модулю значения (х₁ - вообще любые, а х₂ – отрицательные).

Чтобы привести пример ОДП в виде прямой, рассмотрим задачу с единственным ограничением: х₁ - х₂ = 2. Неограниченная ОДП выделена более жирной линией на рисунке 16.

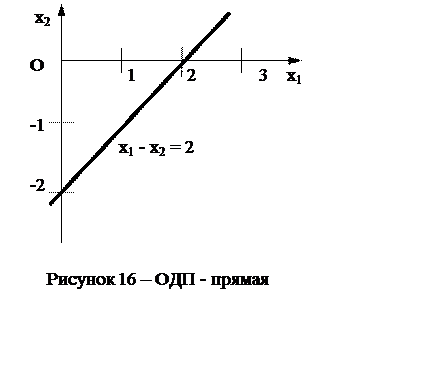
Из проведенных рассуждений видно, что задача линейного программирования может иметь 0, 1 или бесконечное множество оптимальных планов. При этом можно сказать, что любая точка на отрезке между допустимыми планами тоже будет допустимым планом*.

2.2.2 Нахождение оптимального плана

Зафиксировав значение целевой функции равным некоторому числу z, можно построить прямую с₁х₁ + с₂х₂ = z. Эта прямая называется линией уровня целевой функции. Различным значениям z будут соответствовать прямые, параллельные друг другу, причем все они будут перпендикулярны градиенту целевой функции. Координаты градиента будут определяться коэффициентами целевой функции при соответствующих переменных (так как функция линейная, ее частные производные будут константами).

Итак, пусть поставлена задача на максимум (целевая функция максимизируется). Чтобы определить направление роста целевой функции, проведем на графике вектор из начала координат в точку (с₁; с₂) (можно указать направление градиента и любым другим способом). Проведем перпендикулярно градиенту линию уровня и будем сдвигать ее в направлении градиента до крайнего положения. Крайнее положение линии уровня - это такое ее положение, в котором она еще пересекает ОДП, но если сдвинуть дальше, то перестанет ее пересекать.

Точка пересечения крайнего положения линии уровня и ОДП  представляет собой точку оптимума (точку максимума, оптимальный план) Х^* (х₁^*, х₂^*). Координаты этой точки получают путем решения соответствующей системы уравнений.

Значение целевой функции, соответствующее крайнему положению линии уровня, - оптимум задачи (обозначим его z^*). Вычислить это значение можно, подставив оптимальный план в целевую функцию задачи.

Решение задачи на минимум отличается только направлением, в котором сдвигается линия уровня. В этом случае движение происходит против градиента, или в направлении антиградиента (значения координат этого вектора будут противоположными). По своему смыслу это действие будет аналогично умножению целевой функции задачи на -1 и решению этой новой задачи на max.

2.2.3 Разрешимость задачи линейного программирования

Проанализируем разрешимость задачи линейного программирования. Очевидно, что если ОДП пуста, то задача не может иметь решений. В самом деле, если допустимых планов нет вообще, невозможно выбрать из них оптимальный.

Если ОДП ограничена, то задача всегда разрешима. Для случая двух переменных это достаточно очевидно. Для задачи линейного программирования в общем виде это утверждение тоже верно.

Если ОДП не ограничена, то задача в некоторых случаях разрешима, а в некоторых нет.

Например, рассмотрим задачу, ОДП которой была построена на рисунке 13. Если при этом целевая функция по-прежнему максимизируется, то найти оптимальный план невозможно. В самом деле, можно сдвигать линию уровня в направлении градиента до бесконечности, и при этом она всегда будет пересекать ОДП. Крайнего положения этой линии не существует, т.е. условия позволяют получить сколь угодно большую прибыль. Целевая функция задачи не ограничена. Поэтому невозможно указать тот допустимый план, который даст максимальную прибыль, и задача будет неразрешима.