Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 7

Здесь первый ряд имеет имя «0,8х₁ + 0,5х₂ <= 800» и построен по точкам, абсциссы которых записаны в первой строке электронной таблицы, а ординаты – во второй (т.е. по точкам (0; 1600), (100; 1440) и (300; 1120)). Второй ряд имеет имя «0,2х₁ + 0,4х₂ <= 600» и построен по точкам, абсциссы которых те же, а ординаты записаны в третьей строке (т.е. по точкам (0; 1500), (100; 1450) и (300; 1350)). Третий и четвертый ряды построены аналогично (см. таблицу 2).

Полученный вариант диаграммы очевидно является неудачным: хочется продолжить некоторые построенные линии дальше, до их пересечения друг с другом и с горизонтальной осью. Для этого в ячейку D1 вместо числа 300 введем, например, 3000. При этом изменятся все результаты расчетов в столбце D, и диапазон исходных данных для диаграммы примет вид таблицы 3.

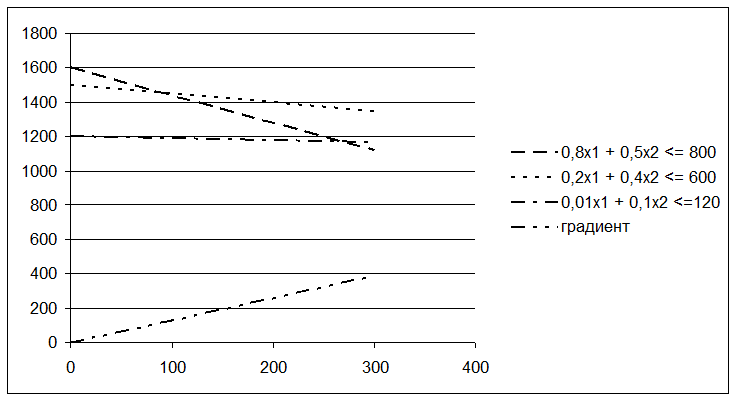
Рисунок 19 – Диаграмма. Вариант 1

Таблица 3 – Диапазон для построения диаграммы. Вариант 2

При этом автоматически перестроится построенная диаграмма. Она примет вид, представленный на рисунке 20.

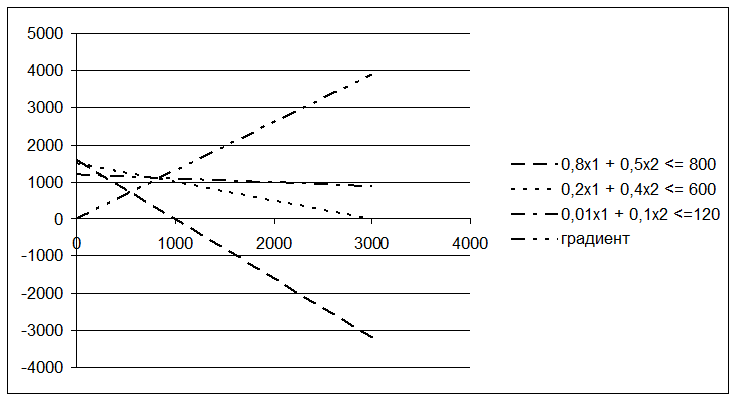 Рисунок 20 – Диаграмма. Вариант 2

Теперь можно предполагать, что на диаграмме видны все точки пересечения, которые могут понадобиться для решения задачи. Однако, диаграммой по-прежнему неудобно пользоваться. Ее следует отредактировать.

Прежде всего, выделим и удалим линии горизонтальной сетки.

Затем отформатируем оси. Для этого ось выделяют и в контекстном меню, которое вызывается нажатием правой кнопки мыши, выбирают пункт «Формат оси». В данном случае в «Формате оси» наиболее важной является закладка «Шкала». Форматируя горизонтальную ось, удобно установить минимальное значение на шкале 0, а максимальное – 1500. Для вертикальной оси установим шкалу от 0 до 1600. Значения координат, лежащие за этими границами, при решении задачи не понадобятся.

После этого проверим масштаб полученного графика. Это можно сделать разными способами, например, как описано далее. Выделим диаграмму и воспользуемся кнопкой «прямоугольник» на панели «Рисование», удерживая клавишу Shift (последнее делается для того, чтобы получить квадрат). Построим квадрат, левый нижний угол которого будет находиться в начале координат, а длина стороны будет равна, например, 1000 по горизонтальной оси.

Результат всех описанных действий представлен на рисунке 21.

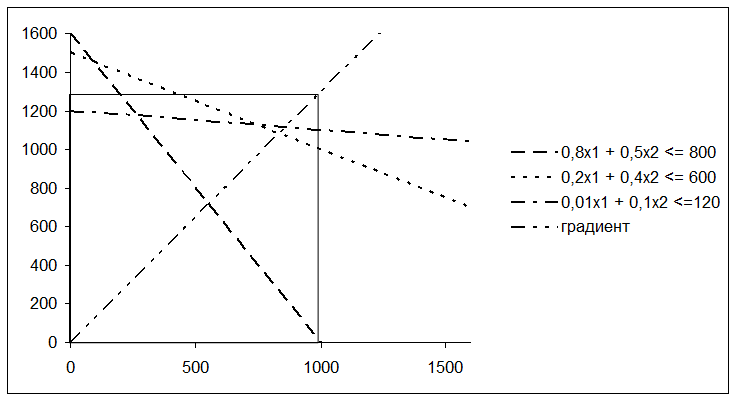 Рисунок 21 – Диаграмма с проверкой масштаба (масштаб неправильный)

Из рисунка 21 видно, что при построении графика нарушен масштаб (1000 т по горизонтали значительно «длиннее», чем по вертикали).

Следовательно, диаграмму надо сделать более «узкой» по горизонтали или «широкой» по вертикали. Для этого диаграмму выделяют и подводят курсор мыши к черным отметкам на рамке области диаграммы таким образом, чтобы он принял вид двусторонней стрелки. Затем, удерживая нажатой левую кнопку мыши, изменяют масштаб диаграммы. После такого изменения его снова следует проверить, и так до тех пор, пока масштаб по осям не станет правильным.

Кроме того, нежелательно, чтобы градиент был изображен через всю диаграмму (в этом случае его трудно отличить от ограничений). Чтобы «укоротить» его, удалим в электронной таблице содержимое ячейки D5. Однако, после этого вектор на диаграмме становится слишком «коротким». Чтобы исправить это, введем в C1 вместо 100 число, например, 250. При этом результаты расчетов в столбце С автоматически изменятся, диапазон данных примет вид таблицы 4, а диаграмма будет выглядеть так, как показано на рисунке 22.

Таблица 4 – Диапазон для построения диаграммы. Вариант 3