Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 8

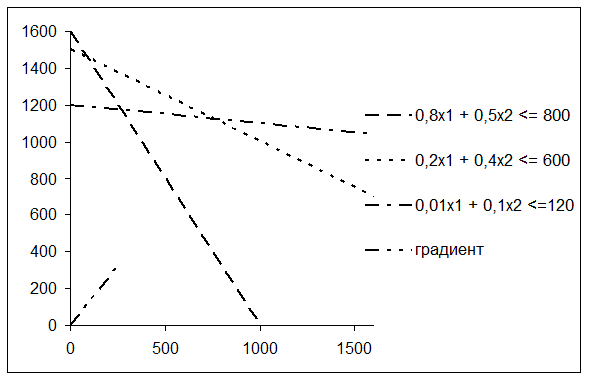
Рисунок 22 – Диаграмма. Вариант 3

Теперь построенной диаграммой удобно пользоваться. Найдем ОДП задачи, как это было описано в разделе 2.1. Соответствующие рассуждения проиллюстрируем на диаграмме, пользуясь инструментами панели «Рисование». При этом следует помнить, что прежде чем изобразить на диаграмме любой элемент этой панели, следует выделить область диаграммы путем однократного нажатия левой кнопки мыши на белом поле диаграммы. Если не сделать этого до обращения к «Рисованию», то построенный элемент не будет частью диаграммы (при дальнейшем редактировании или перемещении диаграммы он «потеряется» на листе Excel).

Для того чтобы обвести ОДП задачи на графике, удобно воспользоваться таким пунктом меню панели «Рисование», как «Автофигуры\Линии\Полилиния». «Полилиния» позволяет изобразить как ломаную линию, состоящую из отрезков, так и любую другую кривую. В первом случае при рисовании линии следует отпускать левую кнопку мыши в каждой вершине ломаной, а во втором – рисовать кривую, не отпуская эту кнопку. Заканчивают рисование незамкнутой ломаной двойным нажатием кнопки мыши. Если ломаная – замкнутая, то рисование будет окончено в тот момент, когда она замкнется. При этом будет предложена автоматическая заливка области внутри этой замкнутой ломаной. Цвет и прозрачность этой заливки можно менять (рекомендуется изменить заливку ОДП на полупрозрачную, чтобы не закрывать другие элементы графика).

В результате диаграмма примет вид, представленный на рисунке 23 (сравните с рисунком 6).

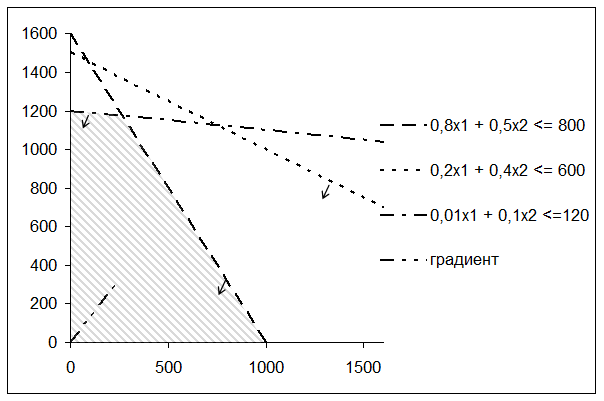
Рисунок 23 – ОДП задачи

Теперь можно найти оптимальный план Х^*. Если сложно представить в воображении положение линии уровня, можно воспользоваться «линией» с панели «Рисование», и в любом месте диаграммы провести перпендикуляр к градиенту. Затем курсор подводят к этой прямой таким образом, чтобы он принял вид крестообразных стрелок и, нажав левую кнопку мыши, перемещают линию уровня в направлении градиента до крайнего положения, как представлено на рисунке 24 (сравните с рисунком 9).

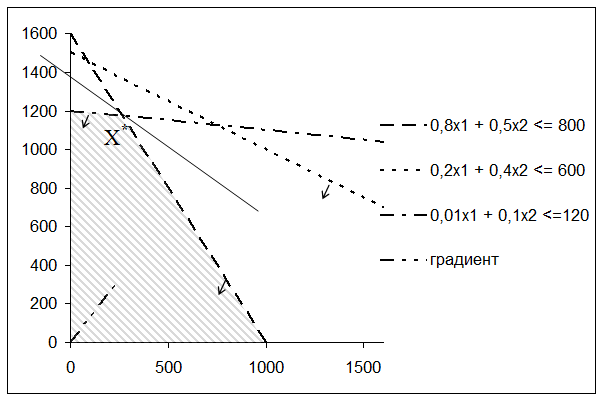
Рисунок 24 – Нахождение оптимального плана

На графике видно, что Х^* – точка пересечения прямых, которые соответствуют первому и третьему ограничениям. Следовательно, чтобы найти ее, необходимо решить систему уравнений:

0,8х₁ + 0,5х₂ = 800

0,01х₁ + 0,1х₂ =120

Для ее решения удобно воспользоваться надстройкой «Подбор параметра» (см. приложение А). Однако эта надстройка предназначена для решения уравнений, а не систем уравнений. Следовательно, надо преобразовать эту систему в одно уравнение с одной переменной.

При построении диаграммы уже использовались формулы, выражающие из этих уравнений х₂ через х₁.

х₂ = (800 – 0,8х₁)/0,5

х₂ = (120 – 0,01х₁)/0,1,

Если вычесть полученные выражения друг из друга, то получим уравнение с одной неизвестной:

0 = (800 – 0,8х₁)/0,5 - (120 – 0,01х₁)/0,1

Каким образом ввести эту формулу в электронную таблицу? Первое и третье ограничения построены по второй и четвертой строкам электронной таблицы. В диапазоне ячеек В2:D2 и В4:D4 уже находятся формулы для х₂. Можно взять любой из этих столбцов и скопировать формулы в любые свободные ячейки. Например, скопируем D2 в Е2, а D4 – в Е4. В результате в Е2 появится формула =(800-0,8*E1)/0,5, а в Е4 =(120-0,01*E1)/0,1. В любую свободную ячейку, например, в Е5 введем разность между этими координатами: =E2-E4. Теперь в ячейке находится формула того уравнения ((800 – 0,8х₁)/0,5 - (120 – 0,01х₁)/0,1), которое необходимо решить относительно х₁. Сама же переменная находится в ячейке E1 (именно на нее ссылаются обе формулы – и в E2, и в E4). Если ячейка Е1 была не заполнена (по умолчанию была нулевой), то столбец Е примет вид, представленный в таблице 5.

Таблица 5 – Подготовка таблицы для использования «Подбора параметра»