Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 3

0,8х₁ + 0,5х₂ = 800

0,01х₁ + 0,1х₂ =120

Отсюда х₁ = 266 2/3, х₂ =1173 1/3.

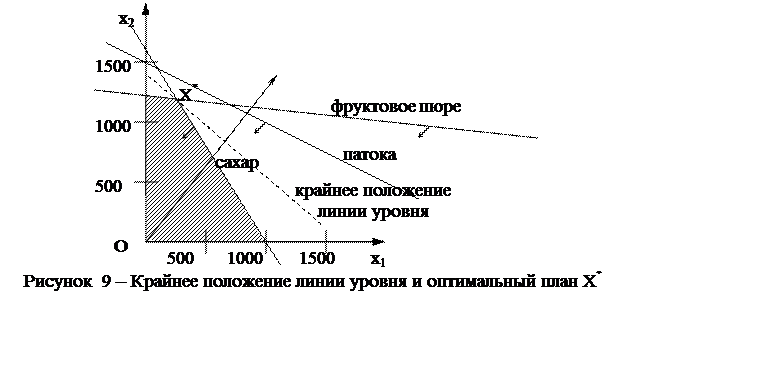
Теперь найдем оптимум задачи, т.е. оптимальную (максимальную) величину прибыли. Для этого подставим найденный план Х^* =
= (266 2/3; 1173 1/3) в целевую функцию задачи: 108х₁ + 140х₂ =108*266 2/3 +
+ 140*1173 1/3 = 193066 2/3.

Ответ задачи: кондитерской фабрике следует выпускать 266 2/3 т карамели «Снежинка» и 1173 1/3 т карамели «Яблочная». При этом ее прибыль составит 193067 руб.

Кроме того, можно сделать из решения задачи некоторые дополнительные выводы. А именно, так как оптимальный план лежит на прямых, которые соответствуют ограничениям по сахарному песку и фруктовому пюре, можно утверждать, что эти ресурсы будут израсходованы полностью (соответственно 800 и 120 т). А вот патока останется в избытке. Если нужно рассчитать неизрасходованный остаток патоки, достаточно подставить оптимальный план в левую часть второго ограничения и определить разность между правой и левой частями.

Рассмотрим теперь общетеоретические основы решения таких задач.

2.2 Геометрическая интерпретация задачи линейного программирования

Рассмотрим задачу линейного программирования с двумя переменными. В общем виде она выглядит следующим образом:

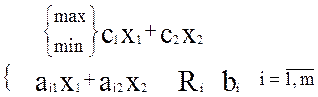
где ;

x_1,2 – переменные;

a_i1, a_i2, b_i, c₁, c₂ - константы;

m – число ограничений.

2.2.1 Построение области допустимых планов

В двумерной системе координат каждое из неравенств системы ограничений определяет полуплоскость с граничной прямой a_i1x₁ + a_i2x₂ = b_i, а уравнение - саму прямую. Пересечение этих полуплоскостей и прямых и представляет собой ОДП задачи.

ОДП задачи может быть:

а) пустой

Это происходит в том случае, если эти полуплоскости и прямые не пересекаются.

Например, предположим, что в задаче из раздела 1.1 требуется произвести не менее 1200 т карамели «Снежинка». Тогда в систему ограничений добавится неравенство х₁ ³ 1200. Ему будет соответствовать полуплоскость, которая не пересекается с четырехугольником, представленным на рисунках 6-9 (т.е. пересечение – пустое множество). График примет вид, представленный на рисунке 10. В самом деле, выделенные ресурсы не позволяют выпустить такое количество карамели, и выполнить поставленные условия невозможно (допустимых планов, действительно, нет).

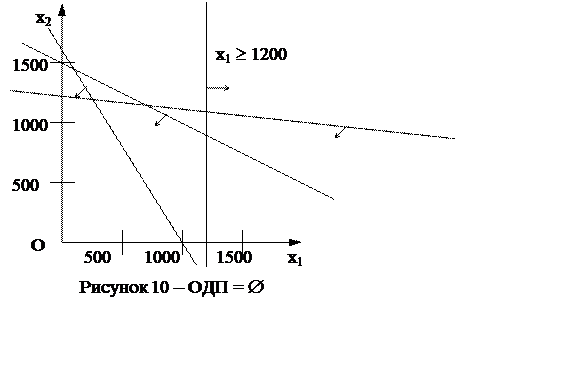
б) непустой

Непустая ОДП может быть:

1   ограниченной

Ограниченная ОДП может быть одномерна (представлять собой отрезок или точку) либо двумерна (представлять собой многоугольник).

Например, ОДП на рисунках 6-9 представляет собой многоугольник (четырехугольник).

Если бы требовалось израсходовать ровно 800 т сахара, не больше и не меньше, то первое ограничение этой задачи представляло бы собой уравнение. Тогда допустимыми планами были бы точки только на соответствующей прямой, а не во всей полуплоскости. ОДП являлась бы отрезком (на рисунке 11 этот отрезок выделен более жирной линией).

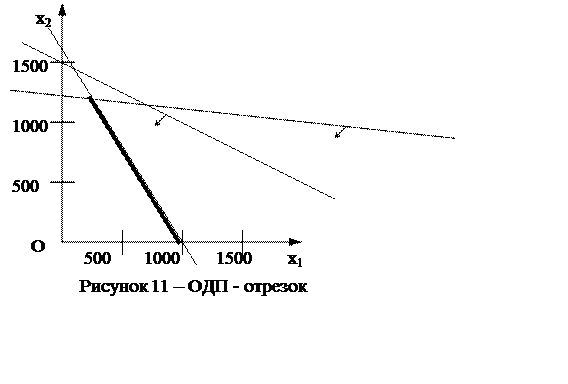
Теперь, например, предположим, что в задаче из раздела 1.1 требуется произвести не менее 1000 т карамели «Снежинка». Тогда в систему ограничений добавится неравенство х₁ ³ 1000. Ему будет соответствовать полуплоскость, которая пересекается с четырехугольником, представленным на рисунках 6-9, в единственной точке (1000; 0) (эта точка выделена на рисунке 12). Эта точка и будет представлять собой ОДП задачи – единственный допустимый план при таких условиях (разумеется, он же будет и оптимальным).

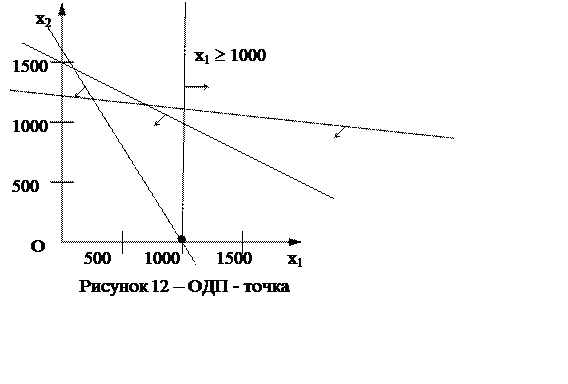
2   неограниченной

Неограниченность ОДП означает, что существуют допустимые планы со сколь угодно большими по модулю значениями хотя бы одной из координат. Неограниченная ОДП также может быть одномерна (луч, прямая) и двумерна (полуплоскость, многоугольная область).

Например, пусть в задаче из раздела 1.1 запасы ресурсов не ограничены, но при этом требуется израсходовать на производство соответственно не менее 800, 600 и 120 т трех видов ресурсов. Тогда в трех неравенствах системы ограничений знак неравенства изменится на противоположный, и система примет вид:

0,8х₁ + 0,5х₂ ³ 800

0,2х₁ + 0,4х₂ ³ 600

0,01х₁ + 0,1х₂ ³ 120

х_1,2 ³ 0

При этом новые неравенства будут определять другие полуплоскости, и область их пересечения примет вид неограниченной многоугольной области. Это и будет ОДП задачи, заштрихованная на рисунке 13.