Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 2

Итак, заштрихованный четырехугольник – допустимые планы, из которых следует выбрать оптимальный, т.е. тот, который даст наиболее высокую прибыль.

Прибыль фабрики определяется по формуле 108х₁ + 140х₂. Зададимся некоторым фиксированным уровнем прибыли. Например, предположим, что нужно получить прибыль 100 000 руб. Все планы производства, которые позволяют получить именно такую прибыль, лежат на прямой 108х₁ + 140х₂ =100000 (назовем эту прямую линией уровня). На рисунке 7 она показана пунктиром под номером 1. Все допустимые планы, которые дают прибыль 100 000 руб., расположены на отрезке этой прямой, который является ее пересечением с ОДП (лежит в заштрихованном четырехугольнике).

Если взять другой уровень прибыли, например, 110 000 руб, то можно получить другую прямую, которая на графике пройдет параллельно первой (в уравнении прямой изменился свободный член, - следовательно, она подверглась параллельному переносу). Таким образом можно изобразить бесконечное множество линий уровня (на рисунке 7 четыре линии уровня показаны пунктиром).

Все линии уровня будут параллельны друг другу и перпендикулярны градиенту целевой функции.  Именно вектор-градиент показывает, в каком направлении растет уровень функции (в данном случае, уровень прибыли).

Координаты градиента представляют собой частные производные функции в точке. Поскольку здесь целевая функция линейная, градиент в любой точке будет одним и тем же. В самом деле, частная производная функции (108х₁ + 140х₂) по х₁ будет равна 108, а по х₂ – 140. Таким образом, координаты градиента (108; 140).

Изобразить такой вектор на плоскости можно различными способами. В геометрии координаты вектора определяются разностью между координатами его конца и начала. Поэтому можно соединить, например, точки (10; 10) и (118; 150); или точки (0;1000) и (108; 1140); или точки (2,1; -5) и (110,1; 135) или т.п.; - координаты всех этих векторов будут (108; 140). Изобразить градиент можно бесконечным множеством способов. Однако удобнее всего с точки зрения вычислений взять в качестве начала этого вектора точку (0; 0), а в качестве конца (108; 140).

В этой задаче нас будет интересовать только направление вектора, а не его длина. Вектор (108; 140) в масштабе построенного графика будет слишком маленьким, и графиком будет неудобно пользоваться. Поэтому изобразим более длинный вектор, умножив обе координаты на одно и то же число (направление вектора при этом не меняется). Например, умножим их на 10. После этого изобразим на рисунке 7 направление градиента целевой функции задачи в виде вектора (1080; 1400). Для этого соединим начало координат с точкой (1080; 1400) (хотя можно было бы построить этот вектор и любым другим способом).

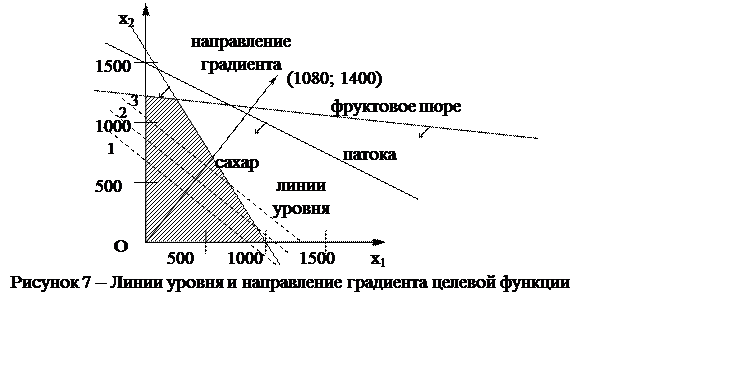
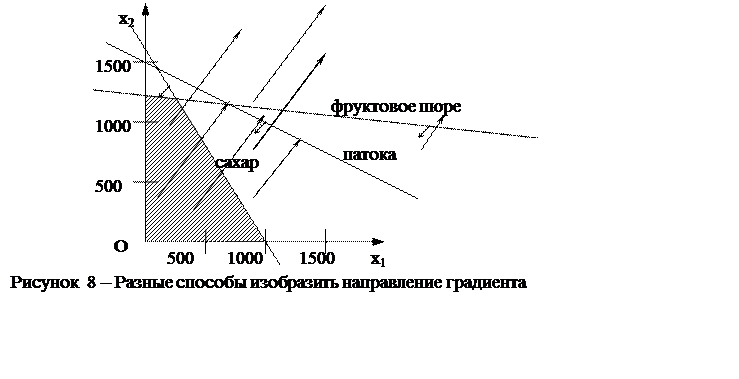
Чтобы еще раз подчеркнуть, что вектор, изображенный на рисунке 7, представляет собой своего рода научную абстракцию, различные другие способы изобразить направление градиента показаны на рисунке 8.

Направление градиента на рисунке 7 показывает, что линия уровня под номером 3 соответствует более высокому уровню прибыли, чем под номером 2, а уровень 1 - еще ниже. Из тех линий уровня, которые изображены на рисунке 7, линии под номером 4 соответствует наиболее высокая прибыль. Однако, такую высокую прибыль невозможно получить, так как линия 4 нигде не пересекает ОДП (нет допустимых планов, дающих такой уровень прибыли).

Поэтому, чтобы найти оптимальный план, мы зрительно «сдвигаем» линию уровня в направлении градиента, но не до бесконечности, а до так называемого крайнего положения. Это такое положение, в котором она еще пересекает ОДП, но если сдвинуть ее чуть дальше, то перестанет ее пересекать (рисунок 9). Крайнее положение линии уровня соответствует самому высокому уровню прибыли, который только можно получить.

Как получить такой уровень прибыли? Нужно найти тот допустимый план производства, который его дает. На графике в этой задаче такой план – единственный. Это точка пересечения ОДП и крайнего положения линии уровня. На рисунке 9 она обозначена Х^* и представляет собой оптимальный план задачи.

На графике видно, что Х^* – точка пересечения прямых, которые соответствуют ограничениям по запасам фруктового пюре и сахарного песка. Следовательно, чтобы найти ее, необходимо решить систему уравнений: