Геометрическая интерпретация и графический способ решения задачи линейного программирования, страница 5

Предположим теперь, что в условиях той же задачи числа 108 и 140 представляют собой не прибыль от тонны карамели, а, например, затраты труда в человеко-часах на производство одной тонны. Необходимо минимизировать общие трудозатраты: min (108х₁ + 140х₂). Тогда линия уровня будет сдвигаться не в направлении градиента, а против него, и можно будет определить ее крайнее положение. На рисунке 17 пунктирной линией показано крайнее положение линии уровня, дальше которого ее невозможно сдвинуть против градиента, так как тогда она перестанем пересекать ОДП. Оптимальный план представляет собой точку пересечения прямых, которые соответствуют ограничениям по сахарному песку и патоке.

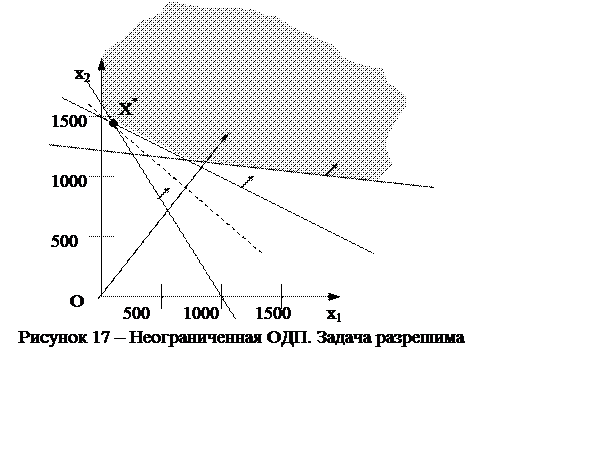
Итак, задача линейного программирования разрешима, если ее ОДП не пуста и ограничена в направлении экстремизации.

2.2.4 Множественное решение

На рисунках 9 и 17 решение задачи являлось единственным. Крайнее положение линии уровня пересекало ОДП в одной точке, следовательно, и оптимальный план был один.

Однако, если градиент проходит перпендикулярно одной из сторон ОДП, оптимальных планов может быть бесконечно много (в этом случае пересечение крайнего положения линии уровня с ОДП может представлять собой всю эту сторону).

Например, предположим, что в задаче из раздела 1.1 прибыль от карамели составляет не 108 и 140 руб. на тонну, а соответственно 160 и
100 руб. Тогда целевая функция примет вид: mах (160х₁ + 100х₂).

Направление градиента этой функции и крайнее положение линии уровня (пунктир) показаны на рисунке 18. При этом видно, что крайнее положении линии уровня полностью совпадает с прямой, которая соответствует ограничению по запасам сахара. Любая точка, которая лежит на этой прямой и в то же время является допустимым планом, будет давать наиболее высокую прибыль (одну и ту же для всех точек) и, следовательно, будет оптимальным планом. Таких планов будет бесконечное множество, и все они лежат на отрезке АВ. На рисунке 18 множество оптимальных планов выделено более жирной линией.

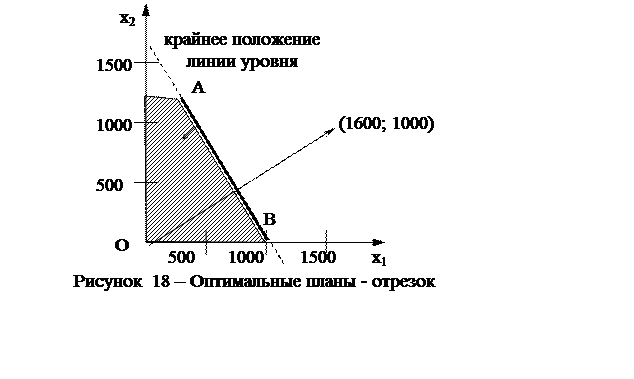
Чтобы убедиться, что совпадение прямых не является результатом неточного построения графика, а имеет место на самом деле, следует сравнить коэффициенты целевой функции – 160 и 100 – с коэффициентами ограничения по запасам сахара – 0,8 и 0,5. В самом деле,160/0,8 = 100/0,5 =
= 20. Коэффициенты этих прямых пропорциональны, следовательно, сами прямые – линия уровня целевой функции и ограничение по сахару – параллельны (при этом они перпендикулярны градиенту целевой функции).

Найдем координаты оптимальных планов. Координаты точки А были найдены в разделе 2.1: А = (266 2/3; 1173 1/3). В = (1000; 0).  Чтобы вывести формулу для любого оптимального плана Х^*, воспользуемся формулой координат отрезка Х^* = k*A + (1 - k)*B = k*(266 2/3; 1173 1/3) + (1 - k)*
*(1000; 0) = (k*266 2/3 + (1 - k)*1000; k*1173 1/3 + (1 - k)*0) = (1000 –
- 733 1/3*k; 1173 1/3*k), где k Î[0; 1].

Подставляя в полученную формулу различные значения k, можно получить различные точки на отрезке АВ. При k = 0 и k = 1 будут получены соответственно концы отрезка B и А. При k = 0,5 будет получена середина отрезка АВ с координатами (1000 – 733 1/3*0,5; 1173 1/3*0,5) = (633 1/3;
586 2/3). При k = 0,1 будет получена точка с координатами (1000 –
- 733 1/3*0,1; 1173 1/3*0,1) = (926 2/3; 117 1/3). Если найти эту последнюю точку на графике, станет видно, что она разбивает отрезок АВ в пропорции 9:1 (находится от точки В на расстоянии, равном ровно одной десятой длины всего отрезка). Таким образом, становится понятен смысл величины k, - она представляет собой ту долю длины отрезка, которая «отсчитывается» от его конца.

Для оптимального плана может быть выведена и другая формула, если взять точку В в качестве начала, а точку А – в качестве конца. Но при подстановке в эту формулу различных значений k все равно будут получены точки на том же самом отрезке.

Итак, чтобы производить карамель оптимальным образом, необходимо выпускать карамель «Снежинка» в количестве 1000 – 733 1/3*k (т), а карамель «Яблочная» - в количестве 1173 1/3*k (т), где k Î[0; 1].

Какую прибыль получит при этом кондитерская фабрика? Обычно для расчета оптимума в целевую функцию подставляют найденный оптимальный план.