Комплекс МУСТАНГ: описание алгоритмов и моделей

 

Описание алгоритмов и моделей

Рига, 2001 год

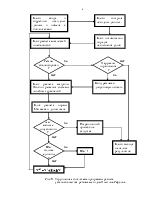
В комплексе МУСТАНГ расчеты установившегося электрического режима выполняются методом Ньютона-Рафсона с улучшением сходимости тяжелых режимов по методу Матвеева. Система линейных алгебраических уравнений решается методом Гаусса с предварительной оптимизацией порядка исключения неизвестных.

Ниже описываются модели элементов электроэнергетической системы, используемые в данной версии программы.

Каждый узел i характеризуется при расчёте стационарного режима следующими данными (см. рис. 1):

·  активной и реактивной нагрузкой (P_нi, Q_нi);

·  напряжением (модулем и фазой- U_i,d_i) в узле;

·  активной и реактивной генерируемой мощностью (Р_гi, Q_гi);

·  активной и реактивной проводимостью на землю, включённой в узле (Y_ia,Y_ir).

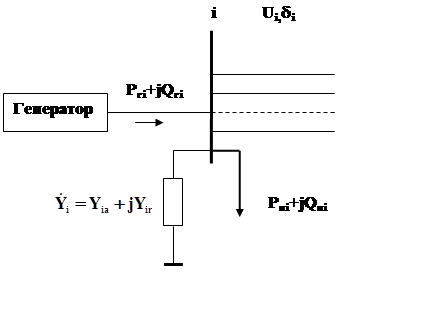Рис. 1. Схема замещения узла i.

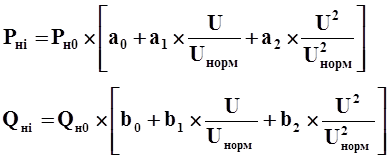где:

Р_н0 и Q_н0                     активная и реактивная состaвляющие мощности нагрузки

при U = U_норм ,

а0, а1, а2             коэффициенты полиномов статических характеристик

активной нагрузки по напряжению,

b0, b1, b2             коэффициенты полиномов статических характеристик

реактивной нагрузки по напряжению.

Реактивная мощность генератора может быть задана фиксированной величиной, либо свободной величиной (с учетом ограничений Q_гmax и Q_гmin).

Каждая связь i-jпредставляется П-образной схемой замещения:

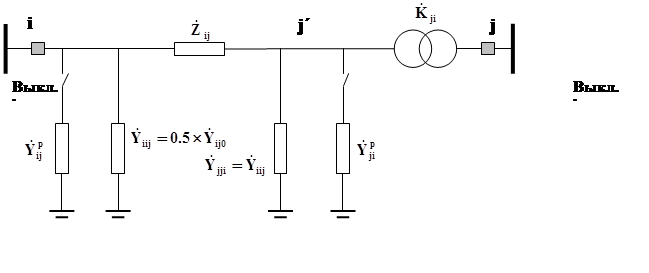Рис. 2. Схема замещения связи i-j.

здесь:

= R_ij + jX_ij                 сопротивление связи,

разнесенная по П-образной схеме замещения, проводимость на землю,

= G_ij0 + jB_ij0

              линейный шунт проводимости у узла i,

              линейный шунт проводимости у узла j,

            комплексный коэффициент трансформации (продольная и поперечная составляющие).

Примечание: в связи может быть только один трансформатор у узла j. Коэффициент трансформации задается отношением напряжения на связи  в точке j' к напряжению узла в точке j:

Обычно в качестве связи, на которой находится трансформатор, выступает сопротивление обмотки трансформатора. Коэффициент трансформации в этом случае определяется как отношение напряжения, к которому приведено сопротивление трансформатора, к напряжению другой ступени. Так, если сопротивление приведено к высокому напряжению, то коэффициент трансформации будет больше единицы, если к низкому, то меньше единицы.

Узлы i и j могут соединяться любым количеством параллельных связей (в том числе и трансформаторных).

Отметим, что для определённости системы уравнений установившегося режима хотя бы одна активная и хотя бы одна реактивная мощности источников не должны быть фиксированы (балансирующие мощности). В общем случае все активные и реактивные мощности могут быть свободными.

Задачей решения установившегося режима является решение системы уравнений:

W (X) = 0,

где уравнения заданы в форме баланса активных и реактивных мощностей в узлах:

Р_гi - P_нi - P_i (X) = 0,

Q_гi - Q_нi - Q_i (X) = 0.

Вектор Х - это вектор зависимых параметров режима. В него входят модули и фазы напряжения в узлах, а также генерируемая активная и реактивная мощности источников.

Р_гi и Q_гi                         соответственно активная и реактивная мощности

источника в узле,

Р_нi и Q_нi                        соответственно активная и реактивная мощности

нагрузки узла.

Сетевые мощности Р_i и Q_i , вытекающие из узла i в сеть, вычисляются по формулам:

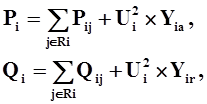где R_i -множество узлов, смежных i-ому.

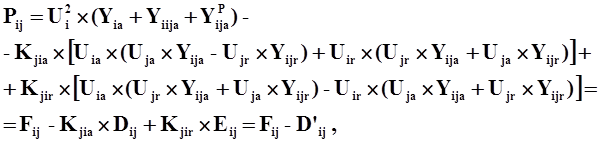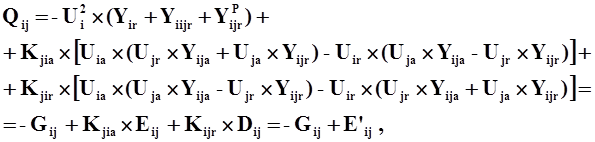где:

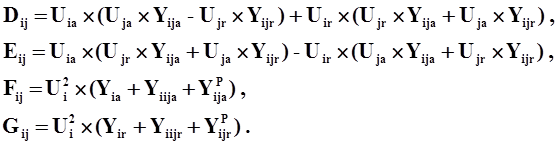Выражения для активной и реактивной мощности для другого конца ветви i-j:

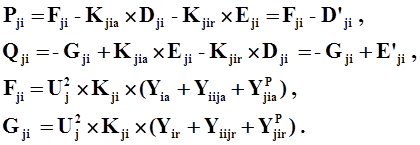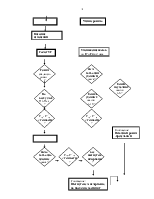
Алгоритм решения системы уравнений W (X) = 0 построен на сочетании метода Ньютона-Рафсона и последовательной деформации уравнений. Итерационная формула данного сочетания методов имеет следующий вид:

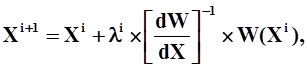где:

Xⁱ, Xⁱ⁺¹               значения вектора зависимых переменных, соответственно,

на i-ом и (i+1)-ом шагах итерационного процесса,

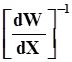
обратная матрица Якоби, вычисленная в

точке X = Xⁱ ,

W (Xⁱ)                  вектор небалансов при X = Xⁱ ,

lⁱ                         коэффициент деформации, определяемый из условий:

lⁱ=1/Kⁱ,   Kⁱ  > B₁ⁱ,   Kⁱ > 1

на каждом шаге вычислительного процесса.

B₁ⁱопределяется выражением:

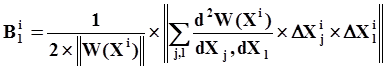где:

норма (т.е. модуль максимальной

компоненты) вектора небалансов,

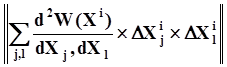норма вектора, получаемого

умножением матрицы вторых

производных дважды на вектор

поправок.

Так как функция W(X) имеет производные не только второго порядка, но и более высоких порядков, то для учета последних вводится связь величин В₁ⁱ и Bⁱ: