Комплекс МУСТАНГ: описание алгоритмов и моделей, страница 11

В свою очередь, система алгебраических уравнений представляет собой систему узловых уравнений большой размерности со слабо заполненной матрицей узловых проводимостей. Для решения этой системы уравнений на каждом шаге интегрирования используется метод Гаусса с предварительной оптимизацией порядка  исключения узлов. Матрица узловых проводимостей обычно комплексная и симметричная (она становится несимметричной в случае хотя бы одного комплексного коэффициента трансформации) и в случае, кода нагрузка представляется характеристикой Y_Н = const, применяется алгоритм ускоренного решения системы линейных уравнений с использованием треугольной матрицы проводимостей.

Если хотя бы в одном узле задан асинхронный двигатель или статический полином изменения нагрузки (или в схеме имеется хотя бы одна ветвь с комплексным коэффициентом трансформации), то на каждом шаге интегрирования производится и прямой и обратный ход по методу Гаусса (с коррекцией Y_Н в тех узлах, где это требуется). В результате этого, время затрачиваемое на расчет переходного процесса возрастает примерно в (2÷2.5) раза по сравнению с предыдущим случаем.

Для решения систем дифференциальных уравнений, применяется комбинация различных методов численного интегрирования:

·  методы Адамса разных порядков,

·  метод, основанный на применении интеграла Дюамеля 3-го рода.

Уравнения движения ротора синхронной машины решаются при помощи метода Адамса 4-го порядка. Общие формулы метода выглядят следующим образом:

для прогноза:

для коррекции:

 

где:

Y_n+1, Y_n                                          значения функции в моменты времени t_n+1,t_n;

значения производных функций в моменты времени

t_n+1,t_n,t_n-1,t_n-2 и t_n-3 соответственно;

h                                      текущий шаг интегрирования h = t_n+1 - t_n;

B₀,B₁,B₂,B₃,B_-1                         коэффициенты, численные значения которых зависят от порядка метода и комбинации предыдущих шагов интегрирования.

Пусть h₁ = t_n-t_n-1,  h₂ = t_n-1 - t_n-2,  h₃ = t_n-2 - t_n-3                 - шаги интегрирования на предыдущих интервалах времени.

Введем следующие обозначения:

тогда расчет коэффициентов B₀, B₁, B₂, B₃ и B_-1 для формул Адамса разных порядков с учетом переменного шага интегрирования выглядит следующим образом:

2-й порядок

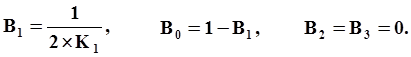Прогноз:

Коррекция:

 

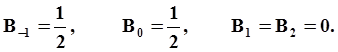3-й порядок

Прогноз:

 

Коррекция:

 

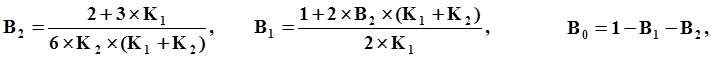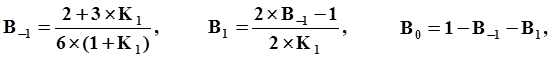4-й порядок

Прогноз:

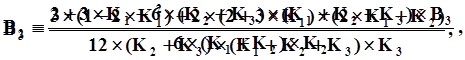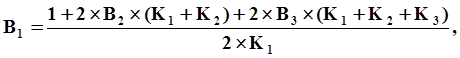Коррекция:

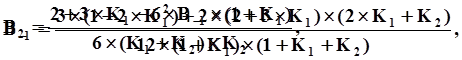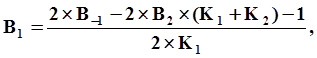Все остальные дифференциальные уравнения синхронной машины, а так же уравнения регуляторов возбуждения и регуляторов скорости можно записать в виде:

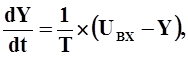где:

T                          -постоянная времени,

U_ВХ                                  -входная "возмущающая" функция.

Решение дифференциальных уравнений такого типа (при линейной апроксимации входной функции U_ВХ) записывается в следующем виде:

здесь:

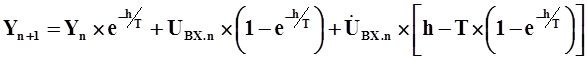          значение входной функции в момент времени t_n,

т.е. в начале интервала интегрирования,

          значение производной входной функции в момент

времени t_n.

Для согласования входных функций исходной системы дифференциальных уравнений производится их повторное вычисление на каждом шаге интегрирования (до 4-х раз).

В генераторных узлах для более точного предсказания вектора напряжения вводится квадратичный полином:

где коэффициенты А и В определяются из следующих условий:

откуда:

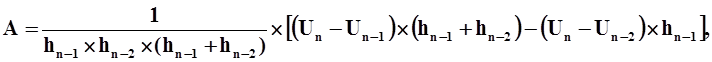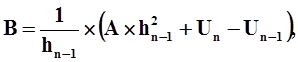где:

U_n+1, U_n, U_n-1, U_n-2            значения напряжения в моменты времени

t_n+1, t_n, t_n-1 и t_n-2, соответственно;

h = t_n+1 - t_n,   h_n-1 = t_n - t_n-1,  h_n-2 = t_n-1 - t_n-2текущий и предыдущие шаги

интегрирования.

Для решения дифференциальных уравнений, описывающих поведение асинхронного двигателя, применяется метод Адамса 3-го порядка с переменным шагом интегрирования.