где ai -некоторые положительные числа, а
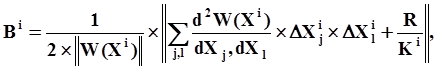
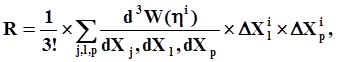 |
Величина B1i в зависимости от знака компонент вектора Rможет быть больше или меньше величины Bi.
Если B1i > Bi , то Ki берется равным B1i,
если B1i < Bi , то Ki выбирается большим Bi ,
т.е. Ki > Bi > B1i.
В большинстве случаев сходимость итерационного процесса будет наилучшей при:
Однако, в тех случаях, когда R достаточно велико, Ki необходимо выбирать опытным путем, исходя из условия:
Ki = K´B1i , где: К = 3, 4, 5,…,
Вычислив Ki, мы тем самым вычислили li = 1 / Ki , т.е. определили длину шага итерационного процесса.
Первые производные от функций небалансов W(X) по зависимым переменным Х, т.е. элементы матрицы Якоби вычисляются на основании следующих выражений:
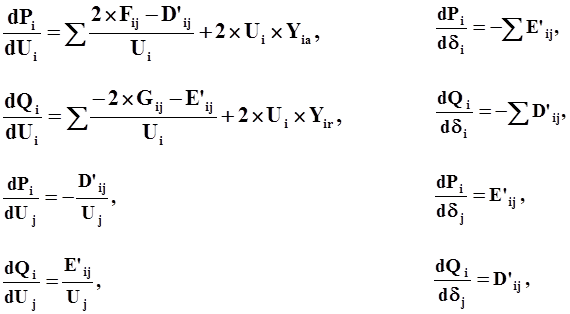
Матрица Якоби формируется построчно по всем i, причем для каждого i формируется пара строк dPi / dXи dQi / dX.
Где: dPi / dX и dQi / dX производные от функций небалансов мощностей
в узлах по всем зависимым переменным
узла i и узлов j, смежных с i.
В строках содержатся только ненулевые элементы матрицы. Каждая сформированная строка имеет вид:
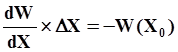 |
Вектор DX получается в результате решения системы линейных уравнений. Для решения этой системы используется метод Гаусса, включающий в себя прямой и обратный шаг. Если решать систему линейных уравнений при произвольном порядке исключения узлов, то в матрице Якоби на промежуточном этапе может появиться много ненулевых элементов. Поэтому после ввода и контроля исходной информации производится топологическая оптимизация схемы с целью определения оптимального порядка исключения узлов.
Для установления оптимального порядка исключения узлов применяются принципы динамического упорядочивания. При иммитационном моделировании прямого хода метода Гаусса, который предшевствует процессу решения линейной системы уравнений, в первую очередь исключается узел, приводящий к появлению наименьшего числа новых связей на последующем шаге исключения. Если таких узлов несколько, то выбирается первый из них по порядку. Это гарантирует экономию оперативной памяти ЭВМ и увеличение быстродействия за счет минимального разрастания матрицы Якоби.
После того как получен вектор поправок DX, рассчитывается коэффициент деформации l. Если l > 1, то принимается l=1, т.е. реализуется метод Ньютона-Рафсона. Если l < 1, то делается поправка к вектору Х в соответствии с формулой:
Итерационный процесс продолжается до тех пор, пока не будет выполнено одно из следующих условий:
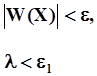 |
где:
εточность расчета стационарного режима,
εl предельно малая величина коэффициента деформации λ.
При выполнении первого условия режим считается сбалансированным. При выполнении второго условия расчет прекращается из-за несходимости итерационного процесса.
Расчёт установившегося электрического режима может выполняться как без учета, так и с учётом ограничений по реактивной мощности на станциях. Учёт ограничений осуществляется фиксацией переменных, вышедших за допустимые пределы, на ближайшем пределе и расфиксацией соответствующих связанных переменных.
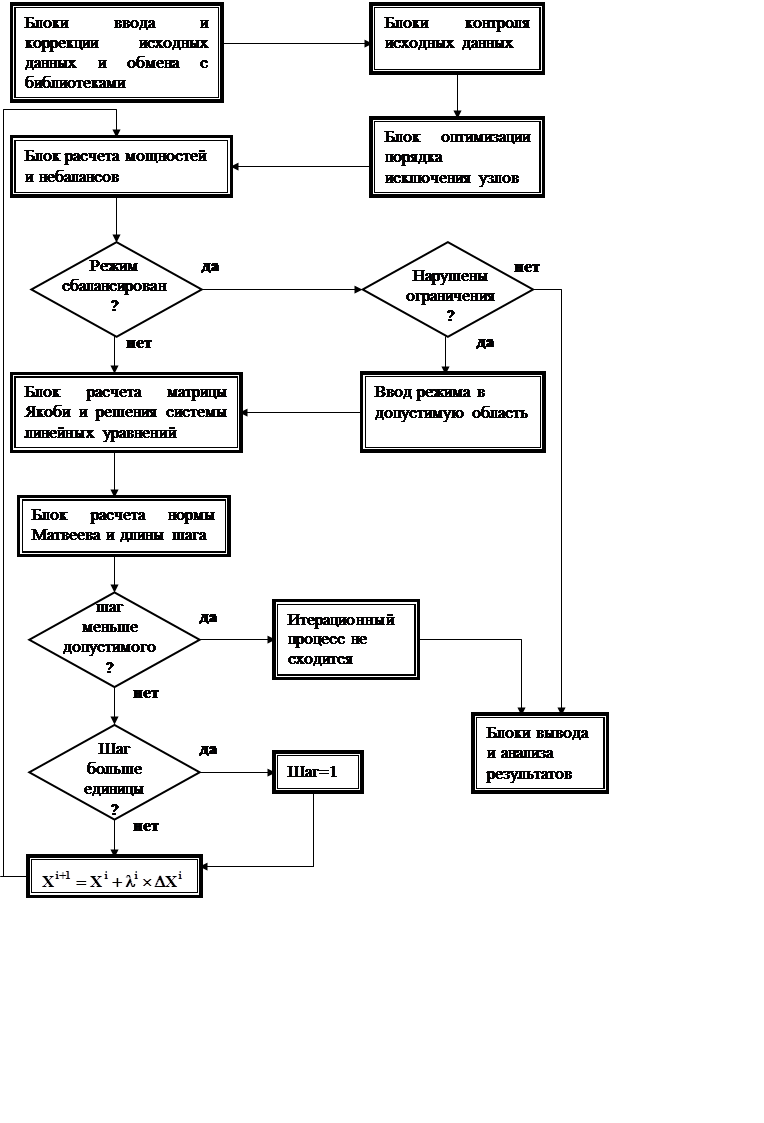
Рис. 3. Укрупненная блок-схема программы расчета
установившегося режима методом Ньютона-Рафсона.
2.Моделирование электромеханических переходных процессов.
2.1.Уравнения основных элементов энергосистем.
2.1.1.Синхронные машины.
Уравнения синхронных машин (CM) соответствуют двум модификациям модели:
· без учета электромагнитных переходных процессов, т.е. с допущением о постоянстве э.д.с. за некоторым реактивным сопротивлением;
· с учетом электромагнитных переходных процессов в контурах ротора.
а) Генератор моделируется постоянством модуля э.д.с. Ег за реактивным сопротивлением Хг.
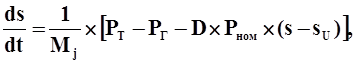 Данная модель генератора описывается уравнениями
движения ротора:
Данная модель генератора описывается уравнениями
движения ротора:
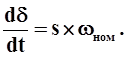
где:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.