Комплекс МУСТАНГ: описание алгоритмов и моделей, страница 3

s                       скольжение ротора СМ относительно синхронно вращающихся осей [o.e.],

δ                      угол ротора СМ, т.е. угол между направлением вектора Ег и синхронно вращаюмися осями [рад.],

ω_ном           синхронная скорость вращения (при частоте равной номинальной, ω_ном=1),

Р_Т          мощность турбины [МВт],

P_Г          электромагнитная мощность СМ [МВт],

Р_ном        номинальная активная мощность СМ [МВт],

M_jмомент инерции СМ вместе с турбиной [МВт×с],

Dкоэффициент демпфирования [о.е.],

s_Uскольжение вектора напряжения относительно синхронно вращающихся осей [о.е.],

б) Генератор моделируется с учетом электромагнитных переходных процессов в роторе при следующих основных допущениях:

·  не учитываются апериодические составляющие переходных процессов в обмотках статора,

·  несимметричные режимы воспроизводятся только токами и напряжениями прямой последовательности,

·  не учитываются изменения в насыщении главной магнитной цепи и зубцового слоя,

·  в продольной и поперечной осях СМ имеется по одному демпферному контуру,

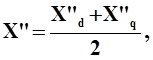·  сверхпереходные сопротивления по продольной и поперечной осям равны, при этом значение сверхпереходного сопротивления Х" вычисляется как

·  здесь дoпустимо полагать X"q=X"d, зависимость X" от ω_U не учитывается.

Уравнения СМ записаны в "форме э.д.с." в осях, жестко связанных с ротором СМ. Эти уравнения соответствуют модели, описанной в "Comparisons of synhronous machine models in the study of the transient behaviour of electrical power systems.", T.J. Hammons, D.J. Winning. -Proc.IEE, vol.118, №10,October,1971. В реализованных уравнениях коэффициент G (см. указанную статью в Proc.IEE) принят равным единице.

Входные переменные:

U_q, U_d                                          проекции напряжения  на поперечную и продольную оси СМ [кВ],

ω_U                                      частота вращения  [о.е.],

E_qe          э.д.с., пропорциональная напряжению, приложенному к обмотке возбуждения [кB],

Р_T                                                          мощность турбины [MBт],

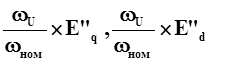
проекции сверхпереходной э.д.с. на оси СМ [кB],

E'_qр                                              формальная переменная (в случае отсутствия демпферных контуров она совпадает с проекцией переходной э.д.с.  на ось q) [кB],

I_d, I_qпроекции тока СМ на оси d и q [кA],

М_Э                                                  электромагнитный момомент СМ [МВт],

s,δ, Р_Г                                то же, что указано выше.

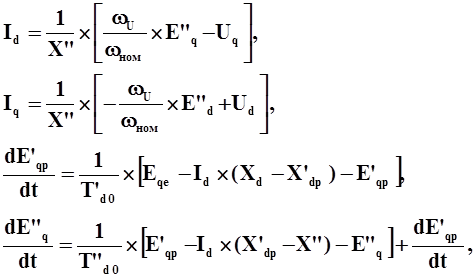Уравнения синхронной машины:

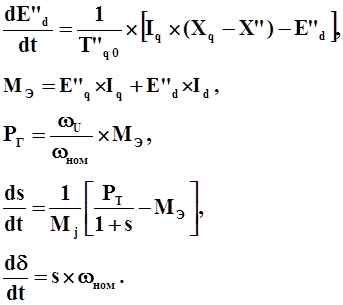
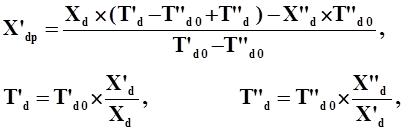где:

электромагнитные постоянные времени T'_d0, T"_d0, T"_q0 заданы в секундах,

коэффициент демпфирования D, который используется в модели E'=const, здесь равен нулю,

величина ω_U во всех случаях вычисляется по уравнению:

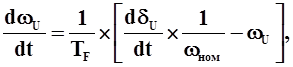
здесь:

δ_U         угол вектора напряжения U относительно синхронно вращающейся оси [рад.],

T_F         формальная постоянная [c].

Синхронный компенсатор (CK).

Уравнения СК отличаются от уравнений генератора следующим:

1) Р_T = 0 ,

2) вместо Р_ном задается S_ном = Q_ном ,

3) M_j задается в МВА×с.

Признаком задания СК в программе MUSTANG является cosφ_ном=0.

Синхронный двигатель (СД).

Уравнения СД отличаются от уравнений генератора следующим:

1) вместо слагаемого Р_T/(1+s) в уравнении движения ротора используется уравнение для момента сопротивления СД:

(c учетом дополнительного момента трогания М_трог)

где:

m_ст               -статический момент сопротивления,

Р_норм             -активная мощность в исходном режиме [МВт],

2) выбег ротора СД ограничивается условием: ω_R больше или равно нулю,

3) в модели с учетом электромагнитных переходных процессов в роторе приближенно учитывается вытеснение тока в демпферных контурах СД. Последнее осуществляется заменой в уравнениях СМ величин T"_d0и T"_q0 на T"_d0/К и T"_q0/К, соответственно. Большей степени вытеснения тока соответствует увеличение коэффициента вытеснения тока К. В общем случае К = К(s'), где: s' = s_U - s.