Методические указания к выполнению лабораторных работ по дисциплине «Процессы и аппараты химической технологии», страница 8

Для сферической частицы по Стоксу:

,

где           – диаметр частицы;

 – вязкость среды;

 – скорость движения частицы.

Опыт показывает, что закон Стокса справедлив для относительно мелких частиц.

Например, при осаждении частиц с плотностью ~ 2000 кг/м³ под действием силы тяжести закон справедлив для частиц  < 65 мкм в воздухе при температуре 20 ºС и для частиц  = 122 мкм в воде при 20 ºС. Оба примера характеризуются весьма малыми скоростями движения. При большой скорости частица своим движением вызывает турбулизацию среды возле нее, т.е. образование хаотических движений отдельных участков, объемов среды, не связанных между собой (рисунок 8).

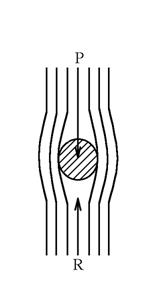
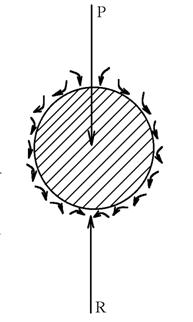
Рисунок 7 – Характер оса-          Рисунок 8 – Характер осажде-

ждения при малой скорости      ния при большой скорости

движения частицы                      движения частицы

В этом случае сопротивление среды обусловлено только инерцией ее перехода из спокойного состояния в движение под действием движущейся частицы. Вместо того чтобы рассчитывать инерцию перехода среды из состояния покоя в движение, удобнее рассматривать равноценную обратную картину перехода кинетической энергии (динамического напора) движущейся среды в давление на неподвижную частицу при скорости среды, равной скорости движения частицы. Этот напор-сопротивление среды можно определить по закону Ньютона для идеальной, не имеющей вязкости жидкости. Для плоской частицы-диска диаметра , расположенного перпендикулярно потоку, сопротивление среды

,

где  – удельный вес среды.

Приведенное выражение, однако, не учитывает всей картины распределения движения струи по ее сечению и вихреобразования как впереди движущейся частицы, так и за ней. Необходимо ввести поправочный коэффициент сопротивления :