Методические указания к выполнению лабораторных работ по дисциплине «Процессы и аппараты химической технологии», страница 2

,                                               (1)

где           – средняя скорость течения жидкости в сосуде (сечение I – I), м/с;

 – средняя скорость течения жидкости в выходном отверстии (сечение II – II), м/с;

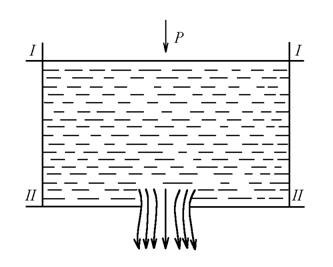
Рисунок 1 – Истечение идеальной жидкости из отверстия

 и  – пьезометрические напоры в сечениях I – I и II – II, м.ст. вытек. жидк.;

 и  – геометрические (нивелирные) напоры в сечениях

I – I и II – II, м.ст. вытек. жидк.;

 – ускорение силы тяжести, м/с².

Как известно, . Так как наружное давление  одинаково для сечения I – I и II – II, то . Скорость  в сечении I – I по сравнению со скоростью в отверстии (сечение II – II) настолько мала, что ее можно считать равной нулю. Учитывая сказанное, уравнение (1) можно переписать так:

или    ,                              (2)

где  – высота столба жидкости в сосуде.

Как видно из уравнения (2), весь движущий напор при истечении расходуется на создание скорости жидкости в отверстии. Это уравнение, представляющее собой частный случай уравнения Бернулли, называется уравнением истечения Торичелли.

Применительно к реальным жидкостям уравнение (2) не дает точных результатов. Опыт показывает, что при истечении реальной жидкости действительная скорость ее всегда оказывается меньшей, чем вычисленная по уравнению (2). Этому явлению можно дать следующее объяснение: при подходе к отверстию в углах сосуда (рисунок