Методические указания к выполнению лабораторных работ по дисциплине «Процессы и аппараты химической технологии», страница 11

Из сказанного следует, что скорость осаждения определяется приравниванием силы сопротивления среды движущей силе:. При осаждении сферических частиц под действием силы тяжести* в условиях применимости закона Стокса:

,

откуда

.

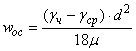Это выражение справедливо, когда  < 1; при осаждении сферических частиц под действием силы тяжести в условиях применимости закона Ньютона:

,

отсюда

.

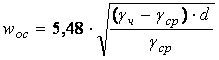Выражение справедливо, когда  > 500. Скорость осаждения частиц в промежуточной области определяется по закону этой области методом последовательного приближения (пробными расчетами), так как искомая скорость входит и в число  и в коэффициент сопротивления . Искомая скорость осаждения та, при которой сопротивление среды

окажется равным движущей силе. Решение задачи упрощается при построении графика:

,

.

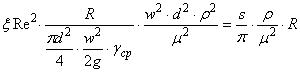В условиях установившейся скорости осаждения вместо силы сопротивления среды в это выражение подставляют равное ей значение движущей силы (). По значению числа  определяют значение  и отсюда – искомую скорость осаждения:

.

При осаждении сферических частиц под действием силы тяжести для установившейся скорости осаждения:

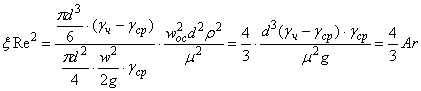
где 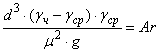   - критерий Архимеда.

Для этого частного случая по графику   можно построить график . По значению числа  по графику определяют число  и отсюда скорость осаждения . Все приведенные выражения для сопротивления среды, а, следовательно, скорости осаждения, справедливы, как указывалось, для шарообразных частиц. В технике, как правило, имеет место осаждение частиц неправильной формы. Очевидно, что коэффициент сопротивления среды  является функцией не только числа , но и формы частиц. В то же время влияние формы на коэффициент сопротивления также зависит от режима движения среды, вызванного движением частицы, т.е. от числа . Вследствие трудности учета влияния формы частицы, расчет скорости осаждения частиц в технологических аппаратах является приближенным.