Ответы на 36 экзаменационных билетов по дисциплине "Алгебра и геометрия"

Билет N1

Матрицы и действия над ними

Пусть даны m*n чисел. Расположим их в виде прямоугольной таблицы, содержащей m строк и n столбцов. Каждое из чисел, входящее в эту таблицу называется элементами матрицы, а сама квадратная таблица называется матрицей порядка m*n.

    Каждому элементу припишем два индекса a_ij i=N строки, j=N столбца.

     Пусть даны две матрицы A и B порядке m*n. Они равны между собой, если для всех i и j выполняется равенство : a_ij = b_ij

     Пусть две матрицы A и B порядка m*n. Под суммой понимается третья матрице C,  элементы которой равны : c_ij = a_ij + b_ij

            A+B=C                        A+B=B+A

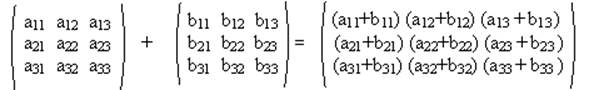
     Пусть дана матрица A, то произведение матрицы A на число понимается матрица, элементами которой являются элементы A*α .

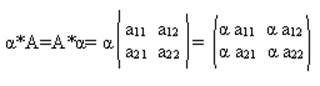
     Особую роль играют квадратные матрицы

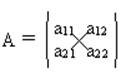
 - главная диагональ (элементы a_ii ), -побочная диагональ.       

 Среди квадратных матриц выделяют единичную матрицу :

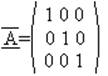
Пусть дана матрица A порядка m*n. Если у этой матрицы поменять местами строки на столбцы, то полученная матрица называется Транспонированной по отношению к A.(A^T)

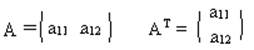
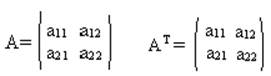
                        Умножение матриц

Пусть дана A m*n и B n*s. Под произведением A*B понимается С: : c_ij =Σ a_in b_nj

A*B=B*A –даже для квадратных матриц.

Билет N2

Определитель- число, полученное из элементов матрицы определенным правилом :

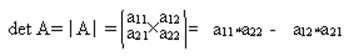
       Если в определителе 3 ого порядка вычеркнуть i-ую строку j-ий столбец, то оставшиеся элементы образуют определитель 2 ого порядка, т е. определитель порядка на 1 меньше исходного.

   ( M_ij ) Минором элемента a_ij - называется определитель, полученный после вычеркивания i-ой строки и j-ого столбца.

    ( A_ij ) Алгебраическим дополнением  элемента a_ij  называется минор, взятый со знаком (-1)^i+j

         A_ij= (-1)^i+j M_ij

     Определителем 3 ого порядка называется число= Σ произведений элементов первой строки на их алгебраическое дополнение.

a₁₁  a₁₂  a₁₃                      

a₂₁  a₂₂  a₂₃      = a₁₁ A₁₁+ a₁₂A₁₂ + a₁₃A₁₃ 

a₃₁  a₃₂  a₃₃                      

       Определителем n-ого порядка называется число=Σ произведений элементов первой строки на их алгебраическое дополнение.

                 Свойства определителей

1 Определитель Матрицы A=Определителю A транспонировано. │A│= │A^T│

│A│= │A^T│

2 Если в определители поменять местами какие-либо 2 строки(столбца) то определитель изменит знак на противоположный.

3 Если в определителе 2 одинаковых столбца(строки),  то он равен 0.

4 Определитель=Σ произведений элементов любой строки(столбца) на их алгебраическое дополнение.                                                                                                                                                          

5 Если элементы какой-либо строки(столбца) имеют общий множитель, то его можно вынести за знак определителя

a₁₁  a₁₂        = K    a₁₁  a₁₂                          

ka₂₁  ka₂₂           ka₂₁  ka₂₂

6 Если элементы какой-либо строки(столбца) представляют собой  Σ 2-х чисел, то такой определитель= Σ 2-х определителей.

a₁₁         a₁₂               =   a₁₁ a₁₂     +     a₁₁ a₁₂                                                                                  

a₂₁+b₂₁  a₂₂+b₂₂            a₂₁  a₂₂         b₂₁  b₂₂

7 Если к элементам какой-либо строки (столбца) определителя прибавить элементы Любой другой строки (столбца) умноженное на любое число, то определитель не изменится.

8 Если в определителе под(над) главной диагональю все элементы=0, то такой определитель= произведению элементов, стоящих на главной диагонали :

a₁₁  a₁₂  a₁₃                      

0  a₂₂  a₂₃      = a₁₁ a₂₂ a₃₃

0  0  a₃₃                      

9 Пусть нам дан определитель. Тогда сумма произведений элементов какой-либо строки(столбца) на алгебраическое дополнение любой другой строки(столбца)=0.

Билет N3

                              Системы линейных уравнений

 Системы m линейных уравнений с n неизвестными, называются системы следующего вида :

    Числа b₁,b₂… b_m– свободные члены

Если в (*) все свободные члены=0, то (*)- это однородная, в противном случае неоднородная.

                  5/x₁+x₂=0 не линейная система

   Решение системы (*)- это всякий упорядоченный набор из n чисел x₁⁰,x₂⁰ , …, x_n⁰, такой, что при его подстановке в каждое из уравнений системы (*) последнее превращается в тождество

        В дальнейшем мы будем рассматривать линейные системы n-уравнений c n неизвестными

   Oопределитель

             a₁₁  a₁₂ … a_1n

                   a₂₁  a₂₂ … a_2n

   ∆  =   …………….     – определитель системы (**)

             a_n1 a_n2 … a_nn    

 Th1 (Крамера)     

        Пусть нам дана система (**). Если ∆(**)≠0, то (**) имеет, и при том, единственное решение, даваемое формулами Крамера :

  x₁=∆x₁/∆     ,x₂=∆x₂/∆ ,…,x_n= ∆x_n/∆

     Где ∆x_k -определитель для неизвестного x_k, которое получается из определителя системы путем замены k-ого столбца свободными членами b₁,b₂,…,b_n