наименование тройки не меняется
a (b
с)= b (c
a)= c (ab)=(a,
b, c)
3 Выражение смешанного произведения через координаты :
a=
axi +ayj+ azk
ax ay az
b= bxi +byj+ bzk (a, b, c)= bx by bz
с= сxi +сyj+ сzk, то cx cy cz
Из того св-ва, что │(a, b, с)│- есть V параллелепипеда сразу следует то, что, для того чтобы три вектора a, b, c были компланарны, необходимо и достаточно, что бы их смешанное произведение= 0
Двойное векторное произведение.
Пусть даны a, b и c. Двойным векторным
произведением называется произведение a(bс)- это вектор лежит в
плоскости сиb
Ясно, что вектор, определяемый двойным векторным
произведением ┴ вектору b
с
Сам же вектор bс ┴ (a, c) –плоскости. A потому очевидно, что данный вектор лежит в плоскости
вектора bиa.
a (bс)=d
a= { ax ; ay; az}
b= { bx ; by; bz }
c= { cx ; cy; cz }
Найдем dx
для этого, прежде всего найдем координаты вектора bc
bc = i j k
ax ay az = (bycz – cybz )i- (bzcx - cxby )j- (bxcy - cxby )k
bx by bz
dx= ay (bxcy - cxby )- az (cxbz - bxcz )= bx (aycy + azcz )- cx (ayby + azbz )=прибавляя и вычитая справа axcxbx получим= bx (axcx + aycy + azcz)- cx (axbx + ayby + azbz)= bx (a c )- cx (a c) т.о.
dx= bx (a c )- cx (a c)
Аналогичным образом легко получить
dy= by (a c )- cy (a c)
dz= bz (a c )- cz (a c)
Т.о. вектор a(bс)={bx (a c )- cx (a b)}i+
{by (a c )- cy (a b)}j+ {bz
(a c )- cz (a b)}k= (bx i+
by j+ bz k)(a c)- (cx i+
cy j+ cz k)(a b)=b(a c)-
c(a b)
T.о окончательно мы получим, что a(bс)=
b(a c)- c(a b)
Билет N13
Аналитическая геометрия пространства.
Плоскость
Ясно, что любая плоскость в пространстве можно определить одним из 2 способов:
1) Точкой Mo(xo,yo,zo) вектором n ={A,B,C} перпендикулярным данной плоскости, который мы будем называть нормалью плоскости.
2) Точками Mo(x,y,z), M1(x1,y1,z1) и M2(x2,y2,z2) не лежащими на одной прямой.
Итак, пусть плоскость, определена точкой Mo и n (1 способ)
Найдем уравнение данной плоскости
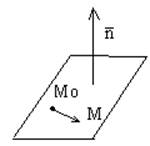
Обозначим через M(x,y,z) произвольную точку плоскости, тогда очевидно, что MoM┴n (ортогональны), а тогда, как известно, скалярное произведение этих векторов=0, т.е. MoM*n=0
Таким образом мы получили векторное уравнение плоскости.
Переходя к координатам полученных векторов получим уравнение плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0
Ax+By+Cz+D=0 (*)
Таким образом всякая плоскость имеет уравнение вида (*), т.е. каноническое- уравнение плоскости(=определяющее).
Ясно, что коэффициент при x, y и z в каноничном уравнении плоскости дают координаты нормального вектора.
Пусть теперь плоскость определена тремя не лежащими на одной прямой точками Mo(xo,yo,zo), M1(x1,y1,z1), M2(x2,y2,z2)
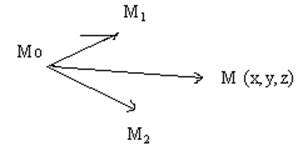Возьмем на этой плоскости M (x,y,z)
Ясно, что вектора MoM2 MoM1 и MoM компланарны, а, как известно, условие компланарности этих векторов:
MoM (MoM1MoM2 )=0
Уравнение плоскости: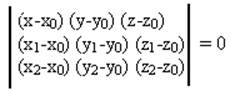 
Билет N 14
Взаиморасположение двух плоскостей
Углом между двумя плоскостями называется линейный угол двугранного угла = угол между нормалями.
Острый угол
Пусть даны 2-е плоскости:
A1x+B1y+C1z+D1=0 (1)
A2x+B2y+C2z+D2=0 (2)
Угол между плоскостями 1 и 2 мы будем называть: острый угол между нормалями к этим плоскостям.
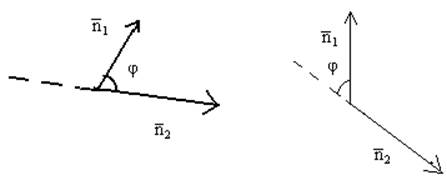
Отсюда легко получить условия параллельности и перпендикулярности двух плоскостей.
Если плоскости параллельны, то n1 и n2 коллинеарные, т.е. n1= λ n2 или
A1/A2 = B1/B2 = C1/C2 = λ
A1/A2 = B1/B2 = C1/C2-условие параллельности
Условие перпендикулярности:
A1A2 + B1B2 + C1C2=0
Билет N 15
Прямая в пространстве.
Ясно, что прямую в пространстве можно определить одним из 3-х способов:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.