Например : ∆x1= ![]()
![]()
![]() b1 a12 … a1n
b1 a12 … a1n
b2 a22 … a2n
∆x1= …………….
bn an2 … ann
Доказательство
Покажем, что (**) имеет решение. Покажем, что числа x1=∆x1/∆ ,x2=∆x2/∆ ,…,xn=∆xn/∆ являются решением (**)
Подставим указанные числа в первое уравнение системы:
a11(∆x1/∆)+a12(∆x2/∆)+…+ a1n (∆xn/∆)=(1/∆)[ a11(b1A11+b2 A21+…+bn An1)+a12(b1A12+b2 A22+…+bn An2)+a1n(b1A1n+b2 A2n+…+bn Ann)]= (1/∆)[ b1(a11A11+a12A21+…+a1nA1n) +b2(a11A21+a12A22+…+a1nA2n)+ bn(a11An1+a12An2+…+a1nAnn)]= (1/∆)[ b1∆+b20+…+ bn0]=
(1/∆) b1∆ =b1 .
Ясно, что проделав аналогичную операцию для оставшихся n-1 уравнений, мы получим ровно n тождеств, что означает, что указанный набор чисел – есть решение (**).
Покажем теперь, что система (**) имеет единственное решение
Пусть x10,x20 , …, xn0 - какое-либо решение (**).
Подставляя это решение в каждое из уравнений (**) мы получим n тождеств :

x10(a11A11+a21 A21+…+an1 An1)+ x20 (a12A11+a22 A21+…+an2 An1)+…+ xn0 (a1nA11+a2n A21+…+ann An1)= ∆x1
∆x10 =∆x1, т.к.∆ ≠0, то x10=∆x1/∆
Аналогичным образом легко показать, что,x20=∆x2/∆ ,…,xn0=∆xn/∆ т.е. получили, что любое решение (**) определяется формулами Крамера, что означает единственность решения ч.т.д.
Билет N4
Рассмотрим однородную систему :

Легко видеть, что система (***) имеет решение x1=x2=x3=…=xn=0, независимо от ∆. Такое Решение называется тривиальным.
Теорема1 Если ∆ ≠0, то (***) имеет только тривиальные решения (по теореме Крамера)
Теорема 2 Если ∆ =0 (***), то (***) имеет, по крайней мере, одно не тривиальное решение.
Доказательство
Для простоты докажем теорему для систем 3-х уравнений с 3-мя неизвестными
Пусть

![]()
![]() a11 a12 a13
a11 a12 a13
∆0 = a21 a22 a23 =0
a31 a32 a33
Предположим, что хотя бы один из миноров 2-ого порядка ≠0.
![]()
![]() Пусть, например, это M22= a11 a13 ≠0
Пусть, например, это M22= a11 a13 ≠0
a31 a33 и перепишем тогда (0) следующим образом :
![]()
Легко видеть, что ∆00-есть M22 ≠0, тогда по теореме Крамера система (00) имеет, и притом, единственное решение
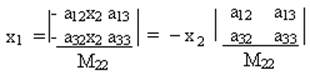
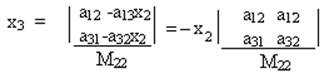
Положим теперь в последнее равенство x2 ≠0, тогда x1,x2,x3-(где x2≠0)-является решением 1-го и 3-го уравнения (0). Покажем, что эта же тройка является решением 2-ого уравнения.
Билет N5
Линейные пространства
Пусть нам дано некоторое множество элементов произвольной природы. Данное множество будем называть линейное пространство, если для элементов этого множества определены операции:
1) Для любых 2-х элементов a и b, принадлежащих этому множеству определена операция сложения : a+b
2) Для любых 2-х элементов a и b, принадлежащих этому множеству определена операция умножения на элемент z : za
Операции подчиняются следующим законам:
1 a+b=b+a
2 (a+b)+c=a+(b+c)
3 В этом множестве существует 0 элементов a+0=a
4 Для каждого элемента a существует обратный элемент (-a)
5 (α+β)a=aα+βa
6 (αβ)a= (βa)α
7 a*1=a
т.o., если над множеством введены операции, подчиняющиеся этим законам, то это линейное пространство.
В дальнейшем обозначим линейное как Z.
Рассмотрим множество всех положительных чисел, если это множество с обычными операциями + их умножение не являются линейными в пространстве.
Покажем, что над элементами этого множества можно вести операции сложения и умножения на число так, что множество станет линейным пространством.
1) a+b=(a(b))
возьмем любую λ и любой элемент a λa=aλ
1 a+b=(ab)=(ba)=b+a
2
3 0=(1) a+0=a=a*1
4 a -a=1/a a+(-a)=a*(1/a)=0(1)
Линейная зависимость и независимость элементов линейного
пространства.
Пусть дано некоторое линейное пространство L, Пусть a1,a2,…,an принадлежат L
Элементы a1,a2,…,an – линейно независимы, если равенство λ1a1+ λ2a2+…+ λnan=0 выполняется тогда и только тогда, когда все λ1+λ2+…+ λn=0. В противном случае будем говорить, что сумма элементов линейна зависима.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.