Свойства линейно зависимых систем
1) Если система элементов a1,a2,…,an – линейно зависима, то хотя бы 1 из элементов этой системы представим в виде линейной комбинации остальных.
Пусть a1,a2,…,an – линейно зависима, тогда равенство λ1a1+ λ2a2+…+ λnan=0 выполнимо, и хотя бы 1 из λ≠0
Пусть λ1≠0, тогда λ1a1= - λ2a2-…- λnan –линейная комбинация
т.к. λ1≠0, то a1= - (λ2/λ1)a2 -…- (λn/λ1)an
2) Если система элементов (a) содержит 0 элементов, то она линейно зависима
Пусть, например a1=0, 1*a1+0*a2+…+0*an=0
Из последнего равенства следует, что система линейно зависима, т. к. 1=λ1≠0
Билет N6
Размерность линейного пространства
Пусть дано некоторое пространство L. Будем говорить, что линейное пространство L- n-мерно если в этом пространстве n линейно-независимых элементов, а любое n+1 не независим.
Если же пространство n-мерно то обозначим Ln.
Пусть дано n-мерное пространство Ln любая упорядоченная система линейно независимых n элементов называется базисом в этом пространстве l1,l2,…,ln-базис.
Теорема
Если l1,l2,…,ln- базис в пространстве Ln то любой элемент l1 принадлежащий этому пространству представим в виде линейной комбинации базисных элементов и это представление единственное.
Док-во.
Пусть a –произвольный элемент принадлежащий L. Тогда система элементов l1,l2,…,ln, a- линейно зависима, т. к. n- элементов линейно независимо, а n+1 линейно зависимо, тогда λ0a+λ1l1+ λ2l2+…+ λnln=0 выполняется равенство и хотя бы 1 из λ≠0 Пусть λ0≠0
Ясно, что λ0 => a= - (λ1/λ0)l1 -(λ2/λ0)l2 -…- (λn/λ0)ln => a представим в виде линейной комбинации. Полагаем, что такое представление единственное.
Предположим, a=α1l1+α2l2+…+αnln (1)
a= β1l1+β2l2+…+βnln (2)
(1)-(2)=0 => (α1-β1)l1+(α2-β2)l2+…+(αn-βn)ln =0
т.к. l1,l2,…,ln-базис, то из равенства =>, что α1=β1, α2=β2 ,…,αn=βn
Билет N 7
Векторы (далее векторы выделены жирным шрифтом)
Вектором называется направленный отрезок, т.е. для него указаны начальная и конечная точки.
![]()
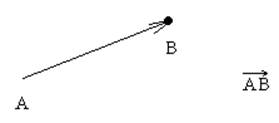
Длина- расстояние от A до B. │AB│
Если даны два вектора a и b, то они коллинеарны (a параллелен b), если эти вектора лежат на одной, или на параллельных прямых.
Они равны (a=b), если они коллинеарны, длинны их равны и соноправлены.
Действия над векторами
1) Сложение Сумма (a+b) - это вектор c, начало которого совпадает с началом a, а конец с концом b,при условии, что начало b совпадает с концом a.
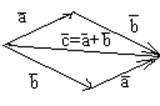
2) умножение на число. a, λ Произведение λ*a называется вектор, длина которого в │λ│ раз больше длиныa. Этот вектор параллелен a. λ*a;a- соноправлены, если λ>0
λ*a;a- противоположно направлены, если
λ<0
Билет N 8
Если даны a и b; b≠0 (не нулевой), то для того, чтобы a был параллелен b, необходимо и достаточно, чтобы существовало λ: a= λb.
Ясно, что введенные операции сложения векторов и (*) на число, делают множество векторов линейным пространством, в чем легко убедится, проверив выполнение известных аксиом.
Рассмотрим множество векторов, лежащих в одной плоскости и покажем, что это множество представляет линейное пространство размерностью 2.
Покажем, что существует 2-а линейно независимых вектора, лежащих в данной плоскости. Действительно рассмотрим a не параллельный b и предположим, что они линейно зависимы, т.е. λ1a+ λ2b=0 имеет место и хотя бы одно из λ ≠0
Пусть λ1a += -λ2b
а= -( λ2/ λ1)b, что означает коллинеарность, что противоречит условию
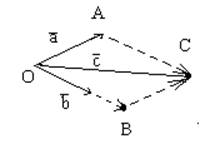
Покажем, что любые 3 вектора, лежащих в данной плоскости- линейно зависимы.
Рассмотрим 3 любых вектора a, b, c. Ни одна из пар не коллинеарная
Построим параллелограмм OACB: диагональ OC совпадают с с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.