Ответы на 36 экзаменационных билетов по дисциплине "Алгебра и геометрия", страница 6

1) Точка Mo(x_o,y_o,z_o) принадлежит прямой и   l   ={m,n,p}параллелен прямой, где   l направляющий вектор.

2) Mo(x_o,y_o,z_o), M₁(x₁,y₁,z₁)

3) Пересечением двух плоскостей.

   Пусть прямая определена 1-ым способом.

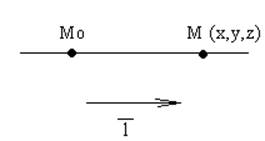
Обозначим через M произвольную точку

Ясно, что вектора  MoM и  l  коллинеарны, т.е. MoM= λ  l.

                    Векторное уравнение прямой.

MoM= λ  l

Координатное уравнение (*):        

           

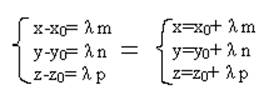
    Система (*) называется параметрическим уравнением прямой в пространстве:

m, n, p  не равны 0.

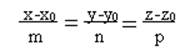     каноническое уравнение прямой в пространстве.

Если p=0, то z-z₀ =0

  Ясно, что одна или две координаты l   могут быть=0. Тогда, например, каноническое уравнение принимает вид:

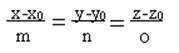    , что означает, что z-z₀ =0, и

    Пусть теперь прямая задается двумя точками Mo(x_o,y_o,z_o) и M₁(x₁,y₁,z₁). Для того, чтобы написать каноническое уравнение прямой надо знать точку, принадлежащею данной прямой (Mo) и направляющий вектор   l  .

  Ясно, что в качестве   l  можно взять  l    =   MoM = {(x₁-x₀);(y₁-y₀); (z₁-z₀)}

Тогда каноническое уравнение:

    

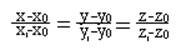
    Пусть задается пересечением двух плоскостей:

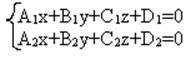
      Для нахождения какой-либо (.) принадлежащей данной прямой, как правило, поступают следующим образом: полагают, что одна из координат (например z=0), тогда для нахождения x_o и y₀  полагают:

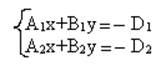    Отсюда находят x_o и y_{0 .}

Найдя Mo(x_o,y_o,z_o), остается найти направляющий вектор. Ясно, что в качестве направляющего вектора  l  можно взять   l =n₁ n₂ (векторное произведение нормалей) и после этого записать каноническое уравнение.

Билет N 16

Взаимное расположение двух прямых и прямой и плоскости.

Пусть даны 2-е прямые:         

                                                      

                                                        

Т.к. углом между двумя прямыми (острым) называется угол между направляющими векторами, то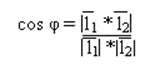

Тогда из полученного выражения легко находим условие параллельности (т.е. l₁ =  λ * l₂ ) и перпендикулярности ( l₁ * l₂ = 0)

Билет N 17

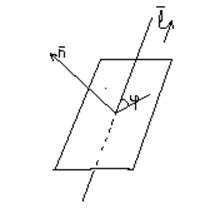Угол между данной прямой и плоскостью называется угол между данной прямой и ее проекцией на плоскость.

     Из определения угла:

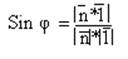
Из полученного выражения получаем условие параллельности прямой и плоскости:   

(n * l)=0 и условие перпендикулярности:   n = λ * l     

Билет N 18

Эллипс- геометрическое место точек, сумма расстояний от которых до двух данных, называемых фокусом, = const

             Теорема: В подходящей системе координат эллипс задается уравнением

,

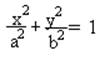  где 2a – сумма расстояний от точек эллипса до фокуса, а  b² = a² – c²  где 2c- расстояние между фокусами.

                                             Доказательство:

      Система координат XOY – называется подходящей, если фокусы эллипса лежат на оси OX, а OY перпендикулярна OX, и проходит через середину расстояния между фокусами.

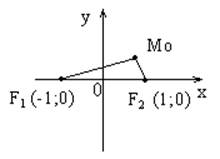Пусть M(x;y)- произвольная точка эллипса

                                            F₁M+ F₂ M=2a

                                            F₁M= ((x-c)²+ y²)^1/2   F₂M= ((x+c)²+ y²)^1/2 

                  ((x-c)²+ y²)^1/2 +  ((x+c)²+ y²)^1/2  =2a

                  ((x-c)²+ y²)^1/2 = 2a-((x+c)²+ y²)^1/2 возведем обе части в квадрат:

                   x²-2cx+c²+ y² = 4a-4a((x+c)²+ y²)^1/2 + x²+2cx+c²+y²

                               4a((x+c)²+ y²)^1/2=a²+cx

Возводя еще раз в квадрат, получим:

a²x+2a²cx+a²c²+a²y²=a⁴+²a²cx+c²x²

( a²   - c² )x²+  a²y²=a² (a²-c²)

Обозначим a²-c² через b² ,окончательно получим:

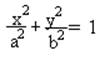
     Доказано, что, если (.) M(x;y) лежит на эллипсе, то ее координаты удовлетворяют последнему уравнению. Для того, чтобы теорема была доказана, осталось показать, что если найдется (.) M(x; y), удовлетворяющая уравнению, то она лежит на эллипсе.

    Пусть нам дан эллипс:

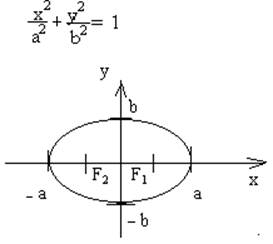Из уравнения видно, что кривая ограничена, т.е. ее можно    поместить в коробочку => │x│≤ a , │y│≤b

      Из уравнения видно, что кривая симметрична относительно оси x и y: (x₀; y₀) (x₀; -y₀)  (-x₀; y₀).

  a и b- полуоси эллипса; a-большая, b-малая –полуоси.

   Если окажется, что в уравнении эллипса a=b, то получим вырожденный эллипс                ( окружность) : x²+ y²=2a.

Билет N 19

2)  Гипербола- геометрическое место точек, разность расстояний от которых до 2х данных точек, фокусов, постоянно.

                                     Теорема (доказать самим).