Ответы на 36 экзаменационных билетов по дисциплине "Алгебра и геометрия", страница 7

   В подходящей системе координат уравнение гиперболы имеет вид :

-каноническое уравнение гиперболы.

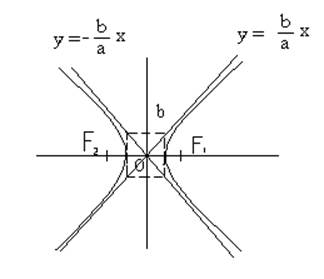где 2a-разность расстояний от точек гиперболы до фокусов.

 b²= c²-a², где 2с-расстояние между фокусами

прямые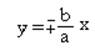 - асимптоты гиперболы

Билет N 20

 Парабола – геометрическое место точек, расстояние от которых до данной точки, называется фокусом= расстояние от этой точки до данной прямой, называется деректриссой

 Теорема :

В подходящей системе координат уравнение параболы имеет вид y²=2px, где p-расстояние от фокуса до деоектриссы.

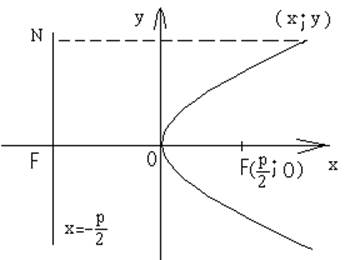Пусть т M (x; y)- произвольная точка парабола

FM=NM

((x-(p/2))² +y² )^1/2= │x+(p/2)│/((x-(p/2))²+y²)

x²-xp+ y²+p²/4 = x²+xp+p²/4

Парабола имеет верхние/нижние ветви  y²=xp

Билет N 23

1. Эллипсоид- поверхность, задаваемая уравнением :

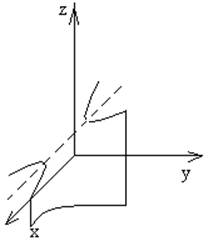
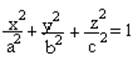Ясно, что она ограничена, т. к. x≤a, y≤b, z≤c

   Для того, чтобы определить форму этой поверхности, применим метод параллельных сечений. Для этого пересечем ее плоскостью :

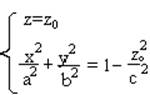в сечении получится кивая. Ясно, что в сечении мы получим эллипс, если │z_o│< 0. Если │z_o│= c, то получим две точки (0; 0; c ) и (0; 0; -c)

   Для того, чтобы определить форму, достаточно произвести сечение этой поверхности, например плоскостью x=0. Для того, чтобы определить кривую, к которой “ прикрепляются” полученные ранее эллипсы :

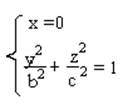Окончательно получаем :

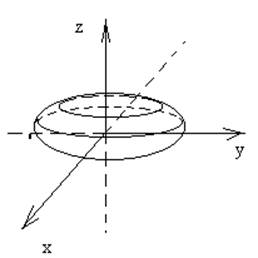Сфера- вырожденный эллипсоид

Билет N 24

2. Однополостный гиперболоид- поверхность задаваемая уравнением :

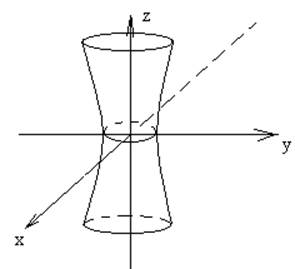
Произведем сечение данной поверхности плоскостями :

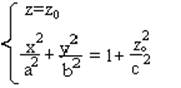сечения –эллипсы

если z_o=0, то сечение- горловой эллипс

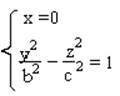 - гипербола

Билет N25

3. Двуполостный гиперболоид :

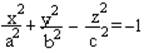
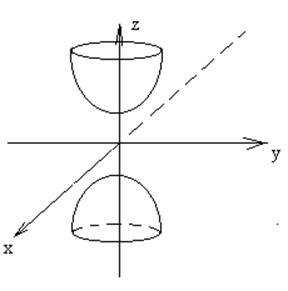
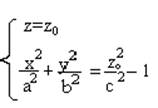- эллипс при │z_o│> c.

  При │z_o│< с   Ø

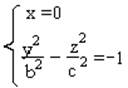
Билет N26

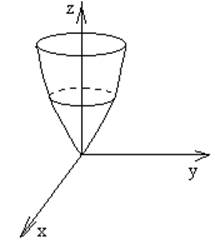
Эллиптический параболоид :

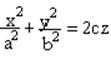
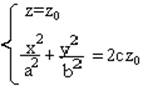- эллипс, если z₀>0 и c>0

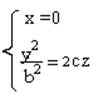- парабола  

Билет N27

4. Гиперболический параболоид :

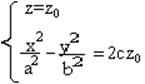- гипербола

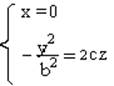- парабола

 Билет N28

                                Комплексные числа

Комплексным числом z называется всякая упорядоченная пара вещественных чисел (a; b) для которых определены алгебраические действия (+,-,,: )

               a=Re z –вещественная часть

               b=Im z –мнимая часть               

z=(a; b)- сопряженное к z

Всякое вещественное число- комплексное, у которого мнимая часть=0

                            a=(a; 0)

   Пара (0;1) обозначается буквой i и называется мнимой единицей  i=(0;1)

Пусть даны 2 к.ч. : z₁ =( a₁; b₁ ) и z₂ =( a₂; b₂ ). Числа z₁ и z₂ – равны (z₁ = z₂), тогда и только тогда, когда  a₁=a₁  и b₁=b₂

Для комплексного числа нет понятия < или >. Они либо=  либо ≠.

      Действия: z₁ =( a₁; b₁ )      z₂ =( a₂; b₂ )

1)  сложения z₁+z₂=( a₁+a₂; b₁+b₂ )-третье к.ч.

2)  вычитание z₁-z₂=( a₁-a₂; b₁-b₂ )-третье к.ч.

3)  умножение z₁*z₂=( a₁*a₂- b₁*b₂; a₁*b₂- a₂*b₁ )

                                i² = -1      i² =(0; 1)(0; 1)=(-1; 0)= -1

      4)  деление  

                   

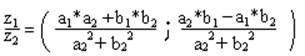
                   z₂≠(0; 1)

      Всякое к.ч. z=(a; b) представимо в виде z=a+bi- такая форма записи называется алгебраической формой к.ч.- такая форма записи называется алгебраической формой к.ч.

       z=(a; b)=(a; 0)+(0; b)=(a; 0)+(b; 0)(0; 1)=a+bi

     z₁+z₂=( a₁+b₁i )+ (a₂+b₂i )=( a₁+a₂ )+ (b₁+b₂)i

      z₁*z₂=( a₁+b₁i)*(a₂+b₂i)= (a₁*a₂- b₁*b₂ )+ (a₁*b₂+a₂*b₁ )i

Степень

i ; i²= -1 ; i³= -i ; i⁴=1       

Билет N29  

                                Геометрическая интерпретация и геометрическая форма к.ч.         

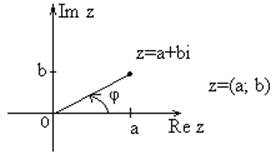
расстояние от ( . ) 0 до ( . ) z – модуль z (│z│)

           │z│=( a²+b² )^1/2      

        φ-arg z (аргумент)

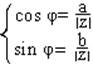
z=│z│(cos φ+ i sin φ)- тригонометрическая форма

Билет N30

Корень n-ой степени из к.ч.

( z )^1/n =(│z│(cos φ+ i sin φ )^1/n =W=│W│(cos ψ + i sin ψ)

     по определению (│W│(cos ψ + i sin ψ))ⁿ=│z│(cos φ + i sin φ)

из равенства двух к. ч. получаем :

   │W│=(│z│)^1/n

 

cos n ψ= cos φ

      sin n ψ= sin φ    => ψ=( φ+2kπ)/n  k=0; ±2;…

(z )^1/n =│z│(cos ( φ+2kπ)/n+ i sin( φ+2kπ)/n), k=0,1,…,(n-1)

     Таким образом (z )^1/n имеет ровно различных значений    

Билет N31

                     Многочлен ( полимер )

Многочленном n-ой степени, целым относительно x – Pn(x), называется выражение a_n xⁿ,

  Pn(x)= a_n xⁿ + a_n-1 x^n-1 +…+ a₁ x + a₀     a_n≠0

   Число x₀  -называется корнем многочлена Pn(x), если при подстановке x₀, мы получаем выражение Pn(x₀)