удовлетворяют условию
![]() , то из сходимости
, то из сходимости 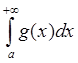 следует сходимость
следует сходимость 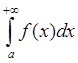 , а из расходимости
, а из расходимости 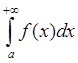 следует расходимость
следует расходимость 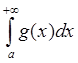
2. Если существует предел  (f(x)>0 и g(x)>0),
то интегралы
(f(x)>0 и g(x)>0),
то интегралы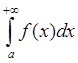 и
и 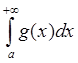 сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Несобственный интеграл II-ого рода (от разрывной функции)
Пусть функция f(x) непрерывна на
промежутке [a;b)
и имеет бесконечный разрыв при x=b. Если существует конечный придел 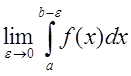 то его называют несобственным интегралом
второго рода и записывают как:
то его называют несобственным интегралом
второго рода и записывают как: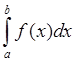 т.е.
т.е. 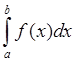 =
=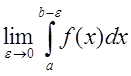
Если предел существует, то интеграл сходится, если не существует или бесконечен, то расходится.
Аналогично, если функция терпит
разрыв в точке x=a, то
полагают 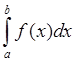 =
=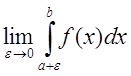 Если
же функция терпит разрыв во внутренней точке с отрезка [a;b], то несобственный интеграл второго рода определяется
формулой:
Если
же функция терпит разрыв во внутренней точке с отрезка [a;b], то несобственный интеграл второго рода определяется
формулой:
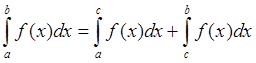
Признаки сходимости:
1. Пусть на промежутке [a;b) функция f(x) и g(x) непрерывны, при x=b терпят
бесконечный разрыв и удовлетворяют условию ![]() .
Из сходимости
.
Из сходимости  вытекает сходимость
вытекает сходимость  , а из расходимости
, а из расходимости  расходимость
расходимость 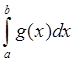 .
.
2. Пусть на промежутке [a;b) функция f(x) и g(x) непрерывны, при x=b терпят
бесконечный разрыв. Если существует придел  ,
то интегралы
,
то интегралы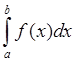 и
и 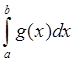 сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
17. Интеграл с переменным верхним пределом.
Th.1 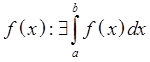
![]()
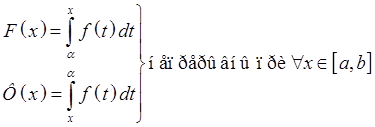
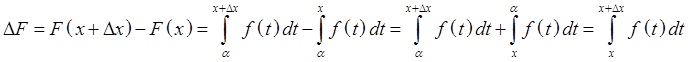
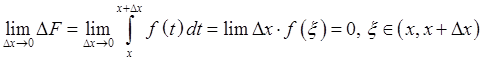
Th.2 Теорема Барроу.
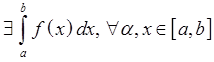

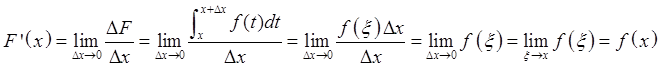
Замечание: 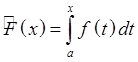
Следствие: всякая непрерывная
f(x) имеет первообразную. Действительно, если f(x) непрерывна на [a,x], то 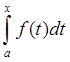 существует, т.е. существует
существует, т.е. существует 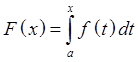 , которая по доказанному является
первообразной.
, которая по доказанному является
первообразной.
Th.3 Формула Ньютона-Лейбница.
Если F(x) – первообразная f(x),
то 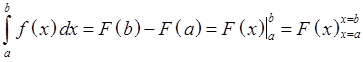
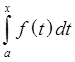 2
любые первообразные отличаются на константу.
2
любые первообразные отличаются на константу.

![]()

 ,
ч.т.д.
,
ч.т.д.
18. Определенный интеграл как предел суммы и его свойства.
Пусть функция определена на отрезке [a,b]. Разобьем отрезок на n частичных отрезков [x0;x1],[x1;x2],…,[xn-1;xn].
![]()
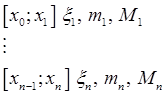
mi – наименьшее значение функции на i-том отрезке
Mi – наибольшее значение функции на i-том отрезке
m – наименьшее значение функции на [a,b]
M – наибольшее значение функции на [a,b]
Составим
нижнюю интегральную сумму: 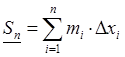 , где
, где ![]() - длина i-того отрезка.
- длина i-того отрезка.
Составим
верхнюю интегральную сумму 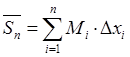
Свойства интегральных сумм:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Составим
интегральную сумму 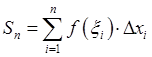
![]()
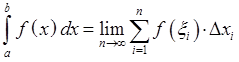 ,
, ![]()
![]() являются частным случаем
являются частным случаем ![]()
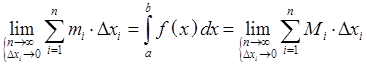
Th.1 Ограниченность интегрируемой функции.
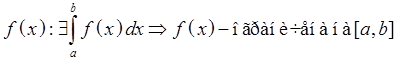
Допустим, что f(x) не ограничена на [a,b]. Покажем, что в этом случае Sn может быть сколь угодно большой.
Пусть
неограниченность f(x) выполняется на ![]()
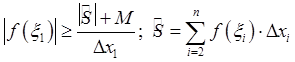
![]() , что противоречит условию, ч.т.д.
, что противоречит условию, ч.т.д.
Обратная теорема не верна.
Достаточное условие интегрируемости разрывных функций:
Th.1 Ограниченная функция, имеющая конечное число точек разрыва на [a,b], интегрируема на [a,b]
Th.2
Ограниченная функция, имеющая конечное число точек разрыва на [a,b],
интегрируема на любом ![]()
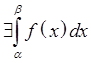
Следствие:
рассмотрим ![]() и пусть
на [a,c]
и пусть
на [a,c] 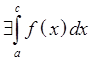

Пределы интегрирования определенных интегралов:
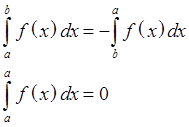
Th. Свойство пределов интегрирования
Для ![]()
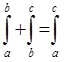
Доказательство:
1) a<b<c смотри выше
2) a<c<b
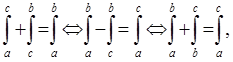 ч.т.д.
ч.т.д.
3) с=а
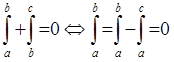
А ещё можно выносить постоянный множитель за знак определенного интеграла, и интеграл суммы равен сумме интегралов.
Th.1 Грубая оценка определенного интеграла.
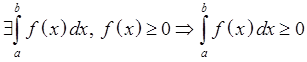
Th.2 Интегрирование неравенств
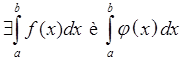
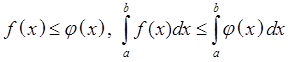
![]()
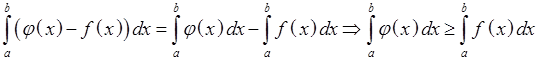
Th.3 Перенесение модуля опр. интеграла под модуль интегрируемой функции
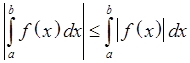
![]()
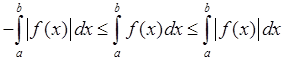
Th.4 Оценка определенного интеграла на m и M
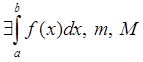

Th.5 Теорема о среднем.
![]()
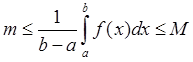
19. Замена переменной в определенном интеграле. Интегрирование по частям.
Th. 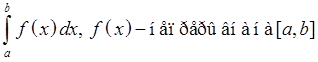
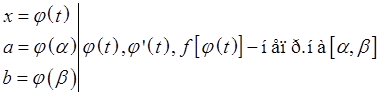
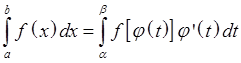
![]()
![]()
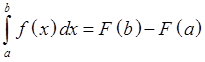
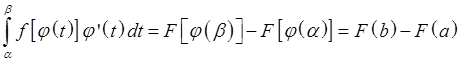
Интегрирование по частям.
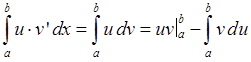
20. Теорема о среднем значении определенного интеграла.
Если
функция f(x) непрерывна на отрезке [a,b], то существует точка ![]() такая, что
такая, что 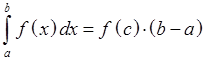
По
формуле Ньютона-Лейбница имеем 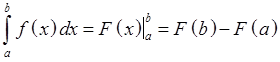 , где
, где ![]()
Применим
теорему Лагранжа о конечном приращении функции, получим ![]()
Число
 называется средним значением функции на
отрезке [a,b]
называется средним значением функции на
отрезке [a,b]
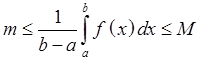
21. Площади плоских фигур. Длина дуги кривой.
1.1 Площадь фигуры в прямоугольных координатах.
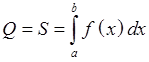 для криволинейной трапеции, ограниченной
f(x) и осью Ox
для криволинейной трапеции, ограниченной
f(x) и осью Ox
 для фигуры, ограниченной сверху f1(x), а
снизу f2(x)
для фигуры, ограниченной сверху f1(x), а
снизу f2(x)
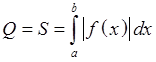 для функций в духе синуса.
для функций в духе синуса.
1.2 Площадь фигуры, заданной параметрически
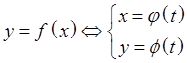
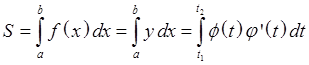
1.3 Площадь криволинейного сектора в полярных координатах.
Сектор
ограничен непрерывной линией ![]() и двумя лучами
и двумя лучами ![]()

2.1 Длина дуги в прямоугольных координатах
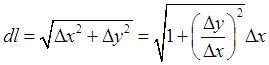

2.2 Длина дуги, заданной параметрически
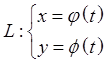
![]()
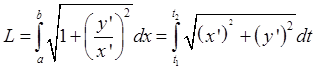
2.3 Длина дуги в полярных координатах
![]()
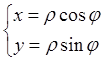
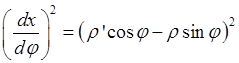
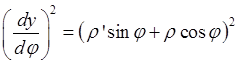
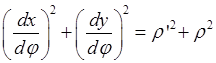

22. Объемы тел
1.Вычисление объема тела по известным площадям параллельных сечений.
1.1
Через произвольную точку ![]() проведем
плоскость, перпендикулярную Ох. Обозначим площадь сечения тела этой плоскостью
S(x). Считаем ее известной и непрерывно изменяющейся. Через v(x) обозначим
объем тела левее плоскости, на отрезке [a,x] он является функцией x.
проведем
плоскость, перпендикулярную Ох. Обозначим площадь сечения тела этой плоскостью
S(x). Считаем ее известной и непрерывно изменяющейся. Через v(x) обозначим
объем тела левее плоскости, на отрезке [a,x] он является функцией x.
1.2
найдем дифференциал dV функции v=v(x). Это элементарный слой, заключенный между
плоскостями x и ![]() , то
есть цилиндр площадью S(x)
высотой dx,
, то
есть цилиндр площадью S(x)
высотой dx, ![]()
1.3 
2. Объем тела вращения.
Пусть
вокруг Ох вращается криволинейная трапеция, ограниченная ![]() . Сечение этой фигуры – круг радиуса
. Сечение этой фигуры – круг радиуса ![]() , следовательно
, следовательно ![]()

23. Приближенное значение определенного интеграла.
1. Метод прямоугольников.

![]()
![]()

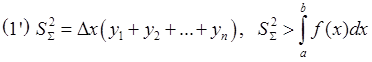
(1) и (1') – формула прямоугольников
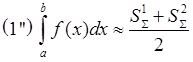
2. Формула трапеций.
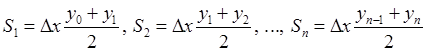
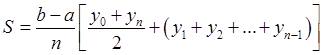
3. Формула парабол (формула Симпсона)
![]()
![]()
Лемма
Площадь трапеции, ограниченной параболой ![]()
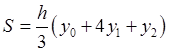

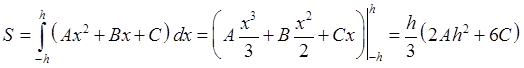

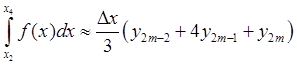
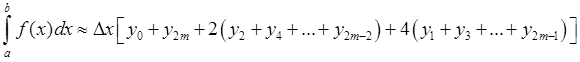
24. Функции нескольких переменных: предел функции, непрерывность, частные производные.
Пусть задано
множество D упорядоченных пар чисел (x,y). Соответствие f, которое каждой паре
чисел ![]() сопоставляет одно и только одно
число
сопоставляет одно и только одно
число ![]() , называется функцией двух
переменных, определенной на множестве D со значениями в
, называется функцией двух
переменных, определенной на множестве D со значениями в ![]() , и записывается в виде
, и записывается в виде ![]() или
или ![]()
Предел функции.
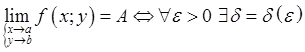
![]()
![]()
![]()
Непрерывность.
![]() - непрерывна в
- непрерывна в ![]()
![]()
1) функция определена в самой точке и вблизи нее
2)
существует предел при ![]() произвольным
образом
произвольным
образом
3) предел функции существует
функция, непрерывная в каждой точке области, непрерывна на всей области
Частные производная.
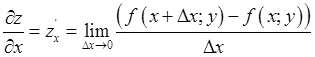 - частная производная первого порядка
- частная производная первого порядка
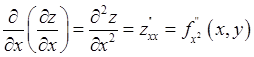 - частная производная второго порядка
- частная производная второго порядка
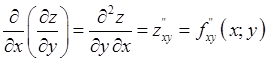 - смешанная ЧП второго порядка
- смешанная ЧП второго порядка
Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
Докажем для производных второго порядка.
Рассмотрим ![]()
![]()
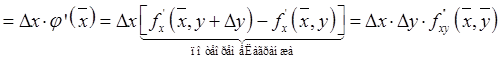
![]()
![]()
![]()
![]()
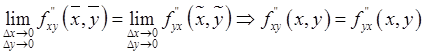
25. Полный дифференциал функции.
Функция
называется дифференцируемой в точке ![]() , если ее
полное приращение в этой точке
, если ее
полное приращение в этой точке ![]() можно
представить в виде
можно
представить в виде ![]() , где
, где ![]() при
при ![]() .
Первые два слагаемых – главная часть приращения функции. Главная часть
приращения функции
.
Первые два слагаемых – главная часть приращения функции. Главная часть
приращения функции ![]() , линейная относительно
, линейная относительно ![]() , называется полным дифференциалом этой
функции и обозначается символом
, называется полным дифференциалом этой
функции и обозначается символом ![]() :
:
![]() . Частные
дифференциалы для независимых переменных полагаются
. Частные
дифференциалы для независимых переменных полагаются ![]() ,
поэтому
,
поэтому ![]()
Th. Если функция дифференцируема в точке ![]() , то она непрерывна в этой точке, имеет в
ней частные производные, причем
, то она непрерывна в этой точке, имеет в
ней частные производные, причем 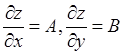 (обратное
неверно)
(обратное
неверно)
Доказательство:
Т.к. функция
дифференцируема в М, то 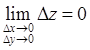 , функция
непрерывна в М. Положим
, функция
непрерывна в М. Положим ![]() , тогда
, тогда 
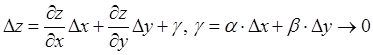 при
при ![]()
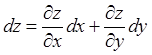
Для функции
n переменных ![]()

26. Дифференцирование сложных функций.
Если ![]() - дифференцируемая в точке
- дифференцируемая в точке ![]() функция и
функция и ![]() -
дифференцируемые функции независимой переменной t, то производная сложной
функции
-
дифференцируемые функции независимой переменной t, то производная сложной
функции ![]() вычисляется по формуле
вычисляется по формуле  .
.
Дадим
независимой переменной t приращение ![]() , тогда
, тогда![]() получат приращения
получат приращения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.