Синтез методом логарифмических частотных характеристик (ЛЧХ) основан на соответствии между ЛЧХ разомкнутой системы и ее статическими и динамическими свойствами в замкнутом состоянии. Для минимально-фазовых систем амплитудная характеристика однозначно определяет характер переходного процесса и нет необходимости вводить в рассмотрение фазовую характеристику. Поэтому при использовании данного метода требуется убедиться, что исследуемая система является минимально-фазовой.
Логарифмические амплитудные частотные характеристики (ЛАЧХ) удобны для синтеза, т.к. их построение, как правило, может выполняться без особой вычислительной работы, а именно, используются асимптотические ЛАЧХ. Поскольку частотные характеристики дают возможность судить о временных характеристиках системы, их знание крайне необходимо при синтезе.
Порядок синтеза методом ЛАЧХ обычно включает в себя следующие операции.
1.Выбор схемы включения корректирующего устройства (КУ) с учетом точности и качества процесса будущей системы.
2.Построение ЛАЧХ неизменяемой (некорректированной) части системы.
3.Построение желаемой ЛАЧХ (ЛАЧХ будущей скорректированной системы), которая удовлетворяет требуемым показателям качества.
4.Графическое нахождение ЛАЧХ корректирующего воздействия (в зависимости от схемы включения КУ).
5.Выбор для полученной ЛАЧХ электрической схемы КУ, нахождение передаточной функции КУ и расчет её параметров.
6.Проверка правильности решения задачи синтеза, а именно, исследование на устойчивость и анализ качества процесса регулирования.
Выбираем схему последовательного корректирующего устройства.
Построение ЛАЧХ двигателя.
Передаточная функция двигателя имеет вид:
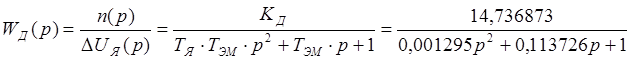
Передаточная функция такого вида может быть у колебательного звена и у инерционного звена второго порядка:
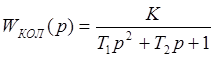 ,
, 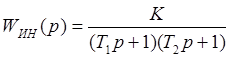 .
.
Находим коэффициент затухания:
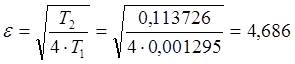 .
.
Так как коэффициент затухания лежит вне диапазона 0,35 – 0,7, передаточную функцию двигателя необходимо привести к виду передаточной функции инерционного звена второго порядка:
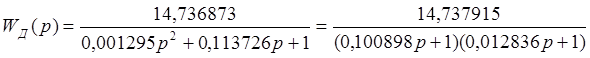
Нахождение значений частоты среза:
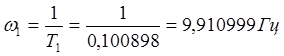 ,
, 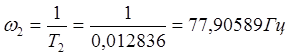 .
.
Нахождение начального значения ЛАЧХ:
![]() .
.
Строим график ЛАЧХ двигателя (рисунок 11)
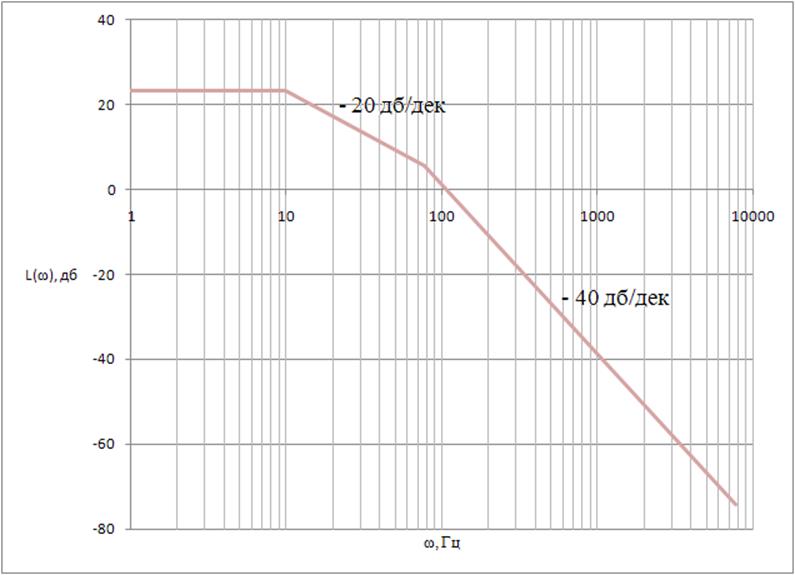
Рисунок 11 – ЛАЧХ двигателя
Построение ЛАЧХ генератора.
Передаточная функция генератора имеет вид:
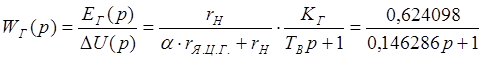
Передаточная функция такого вида
существует у инерционного звена первого порядка.
Нахождение значения частоты среза:
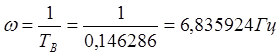 .
.
Нахождение начального значения ЛАЧХ:
![]() .
.
Строим график ЛАЧХ генератора (рисунок 12).
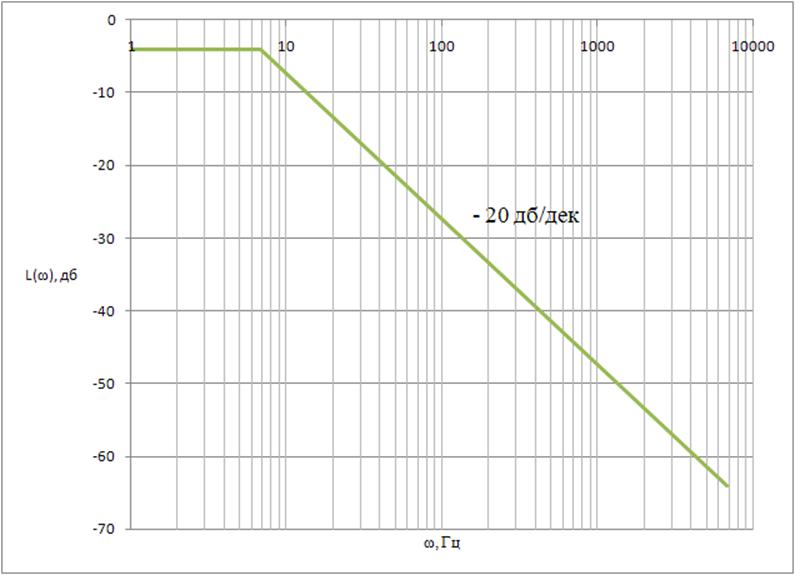
Рисунок 12 – ЛАЧХ генератора
Построение ЛАЧХ тахогенератора.
Передаточная функция тахогенератора имеет вид:
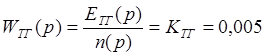
Передаточная функция такого вида существует у пропорционального звена.
Нахождение начального значения ЛАЧХ:
![]() .
.
Строим график ЛАЧХ тахогенератора (рисунок 13).
Рисунок 13 – ЛАЧХ тахогенератора
Построение ЛАЧХ усилителя.
Передаточная функция усилителя имеет вид:
![]()
Передаточная функция такого вида существует у пропорционального звена.
Нахождение начального значения ЛАЧХ:
![]() .
.
Строим график ЛАЧХ усилителя (рисунок 14).
Рисунок 14 – ЛАЧХ усилителя
Построение ЛАЧХ исходной системы.
Так как передаточная функция последовательного соединения элементов равна произведения передаточных функций этих элементов, ЛАЧХ системы равна сумме ЛАЧХ отдельных элементов.
Строим график ЛАЧХ системы (рисунок 15).
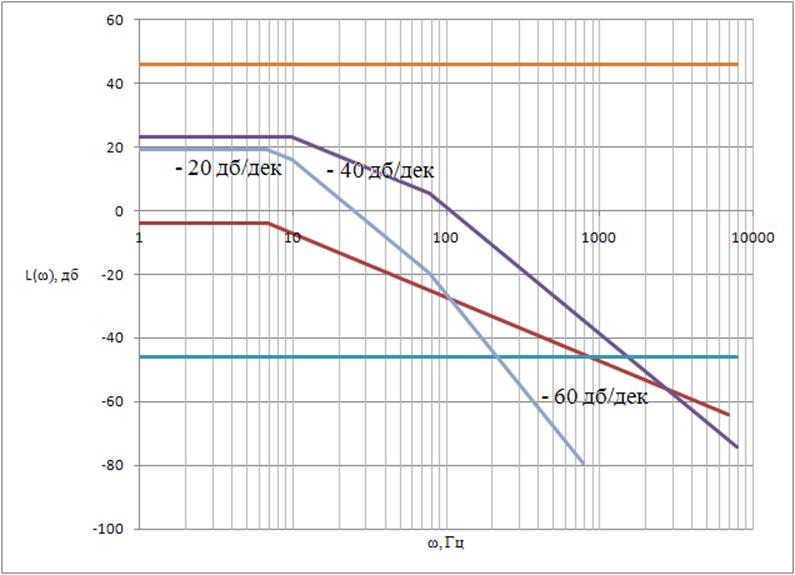
Рисунок 15 – ЛАЧХ системы
2.2 Построение ЛАЧХ желаемой системы
При построении желаемой ЛАЧХ необходимо помнить, что исследуемая система должна быть минимально-фазовой.
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, которая имеет желаемые, требуемые статические и динамические свойства. Желаемая ЛАЧХ состоит из трех асимптот, т.е. участков низких, средних и высоких частот.
При построении желаемой характеристики следует стремиться к совпадению в более широком диапазоне частот с ЛАЧХ некорректированной системы. В противном случае реализация корректирующих устройств существенно усложняется, особенно если речь идет об увеличении частоты среза и повышении коэффициента усиления в области высоких частот.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.