Расчёт системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=1500 об/мин, p=6 кВт), страница 4

.

Вычислим приближенную индуктивность якоря по формуле:

.

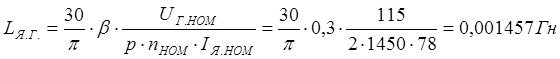Затем находим постоянную времени генератора:

.

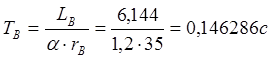Коэффициент передачи генератора равен:

.

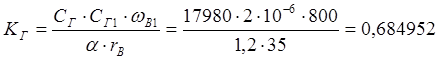Сопротивление нагрузки двигателя:

.

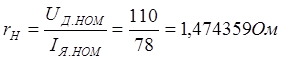Передаточная функция генератора имеет вид:

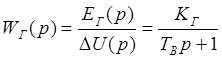
где Е_Г – ЭДС генератора; ∆U – напряжение возбуждения; К_Г - коэффи­циент передачи генератора; T_В – постоянная времени цепи возбуждения.

С учетом нагрузки передаточная функция генератора равна:

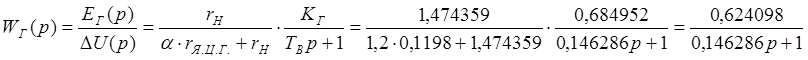
Расчёт передаточной функции тахогенератора.

Исходные данные:

.

Передаточная функция тахогенератора имеет вид:

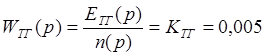
где Е_ТГ – ЭДС тахогенератора; K_ТГ – коэффициент передачи тахогенератора.

1.3  Составление структурной схемы системы и определение передаточной функции АСР

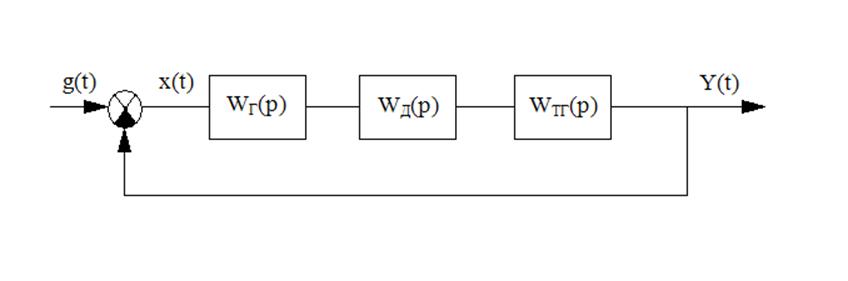
Рисунок 3 – Структурная схема АСР

Передаточная функция генератора с двигателем имеет вид:

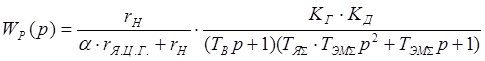
где T_Я∑ – суммарная постоянная времени цепи якоря генератора и двигателя, с, T_ЭМ∑ – суммарная электромеханическая постоянная времени двигателя при работе от генератора, с.

Находим суммарные постоянные времени:

,

.

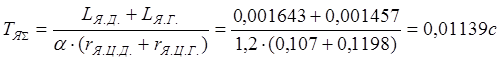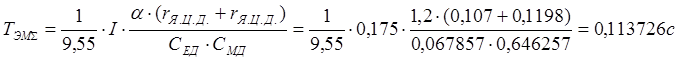Передаточная функция последовательного соединения элементов равна произведению передаточных функций этих элементов.

Передаточная функция разомкнутой системы имеет вид:

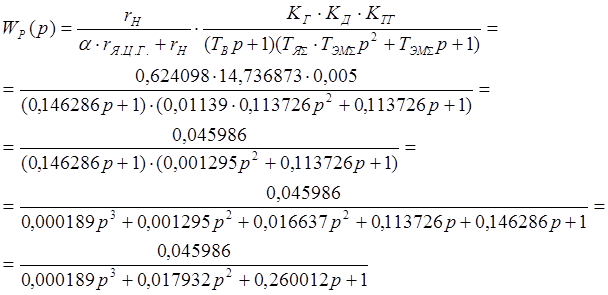
Передаточная функция замкнутой системы имеет вид:

1.4  Исследование устойчивости АСР, расчёт критического коэффициента усиления и выполнение предварительной коррекции системы, исходя из заданной статической точности

Исследование устойчивости системы.

Передаточная функция исследуемой системы в общем ви­де:

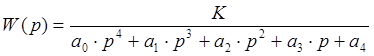
где a₄ = К + 1 — для статической системы; а₄ — К – для астатической (со­держащей интегрирующее звено) системы.

Устойчивость АСР устанавливают по алгеб­раическому критерию Гурвица. Определитель Гурвица для системы 3-го порядка имеет вид:

.

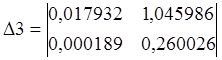Главный определитель Гурвица равен:

,

.

Для того чтобы система была устойчива, необходимо и достаточно, чтобы главный определитель Гурвица и все диагональные миноры были больше нуля при выполнении правила Стодолы.

Правило Стодолы выполняется: все коэффициенты характеристического уравнения одного знака, а именно положительные.

Главный определитель Гурвица и все диагональные миноры больше нуля.

Можно сделать вывод: система устойчива.

Расчёт критического коэффициента усиления.

Для вычисления критического коэффициента усиления следует в определитель вместо а₄ поставить К_КР + 1 либо К_КР в зависимости от вида (статическая или астатическая) системы и, приравняв определитель к нулю, найти К_КР.

Так как система статическая, в её составе нет интегрирующих звеньев, можно заменить а₄ на К_КР + 1 и приравнять главный определитель Гурвица к нулю.

,

.

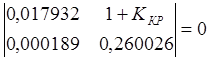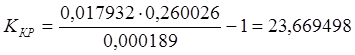Предварительная коррекция системы по заданной статической точности.

По заданной статической точности можно рассчитать необходи­мый коэффициент усиления:

,

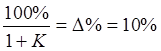где ∆% — заданная статическая точность системы, %.

.

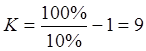Найденный К меньше К_КР, можно произ­вести предварительную коррекцию АСР путем последовательного вклю­чения в систему пропорционального звена с коэффициентом:

.

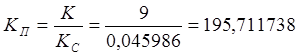где К_С – расчетный коэффициент усиления АСР, равный произведению K_Д, K_Г и K_ТГ.

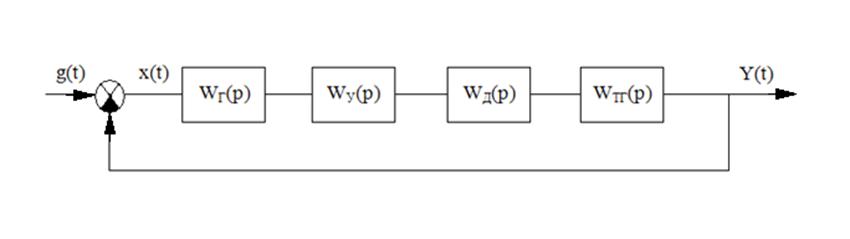
Рисунок 4 – Структурная схема АСР после предварительной коррекции

Передаточная функция системы после предварительной коррекции.

Передаточная функция разомкнутой системы:

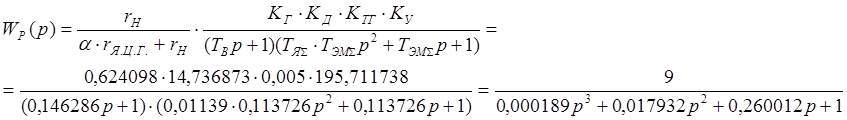
Передаточная функция замкнутой системы:

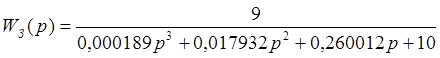
1.5  Расчёт вещественной частотной характеристики заданной системы и построение переходного процесса по задающему воздействию приближённым методом трапеций

Вещественную частотную характеристику (ВЧХ) Р(ω) по­лучает из передаточной функции замкнутой системы путем подстанов­ки в нее р = jω и выделения вещественной части.

Сделаем замену р = jω:

Выделим вещественную часть:

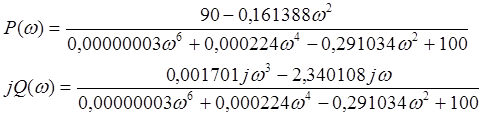
Задаваясь значениями частоты от нуля до бесконечности, находим значения Р(ω). Вносим данные в таблицу.

Таблица 2 – Вещественная характеристика системы