Расчёт системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=1500 об/мин, p=6 кВт), страница 3

Двигатель – П-51:

; ; ; ; ; ;

; ; ; .

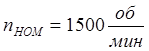Электрический генератор – электромеханическая машина, превращающая механическую энергию вращательного движения в электрическую энергию. Главными элементами двигателя являются: ротор (Якорь) – вращающийся под действием механических сил вал, статор (обмотка возбуждения) – неподвижная часть, двигателя, создающая магнитный поток, приводящий к стеканию с ротора (якоря) электрического тока.

Генератор – П-61:

; ; ; ; ; ;

; ; ; ; .

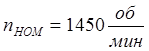Электрический тахогенератор – электромеханическая машина, превращающая механическую энергию вращательного движения в электрическую энергию. Главными элементами двигателя являются: ротор (Якорь) – вращающийся под действием механических сил вал, статор (обмотка возбуждения) – неподвижная часть, двигателя, создающая магнитный поток, приводящий к стеканию с ротора (якоря) электрического тока.

Тахогенератор – АТ-261:

.

1.2  Определение передаточных функций отдельных элементов схемы и расчёт параметров, входящих в соответствующие передаточные функции элементов схемы

Расчёт передаточной функции двигателя.

Исходные данные:

; ; ; ; ; ;

; ; ; .

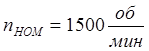Примем приведённый момент инер­ции нагрузки I_Н равным моменту инерции якоря двигателя I_Д. В справоч­ной литературе и каталогах момент инерции часто выражают через ма­ховой момент GD², используя техническую систему единиц МКГСС. В этом случае момент инерции измеряется в кг∙м∙с²:

,

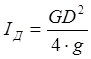где m – масса якоря, кгсс²/м, m – G/g; G – вес якоря (сила тяжести), кгс, G = mg; g —ускорение силы тяжести, g = 9,81 м/с²; 1 кгс = 9,81 кг∙м/с².

Для численного выражения момента инерции I в единицах СИ че­рез маховой момент GD², кг∙м², можно пользоваться соотношением:

.

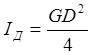Найдём значения I_Я.НОМ, r_Я.Ц.Д. и I_Д:

,

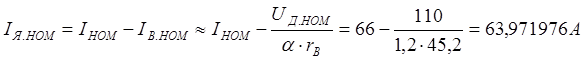2  ,

.

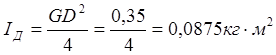Далее определяем постоянные для двигателя:

.

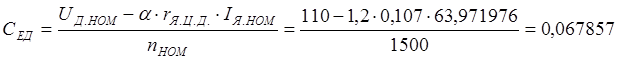где α = 1,2 – коэффициент, учитывающий перегрев обмотки по срав­нению с температурой 15 °С.

Примем, что момент со­противления на валу двигателя не зависит от скорости вращения. Тогда в результате преобразования следующих соотношений:

, ,

, , ,

.

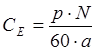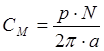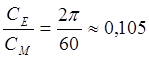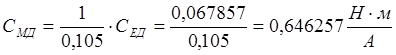Вычислить индуктивность якоря L_Я сложно, поэтому на практике ее определяют экспериментально. Где β = 0,25 – 0,6 (нижнее значение принимается для компенсированных машин, верхнее – для некомпенсированных). Учитывая, что двигатели серии П имеют легкую компенсацион­ную (стабилизирующую обмотку), и полагая β = 0,3, находим:

.

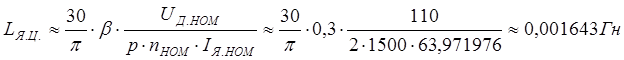Момент инерции на валу двигателя:

.

Подставив численные значения найденных параметров в коэффи­циенты передаточной функции двигателя, получим коэффициент по управляющему воздействию:

,

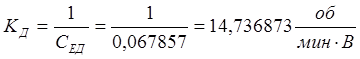коэффициент по возмущающему воздействию:

,

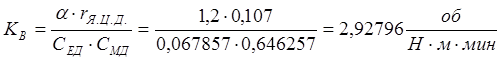и постоянные времени:

,

.

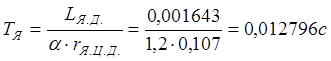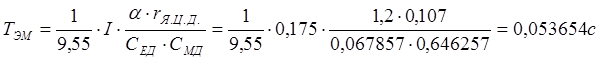Передаточная функция двигателя имеет вид:

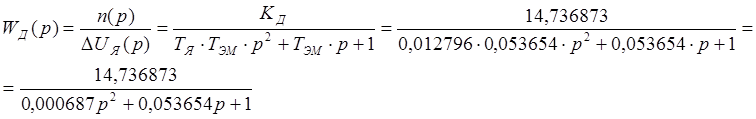
где n – скорость вращения вала двигателя; ∆U_Я – напряжение на якоре двигателя (равно либо E_Г, либо E_ЭМУ); Т_Я – постоянная времени цепи яко­ря; Т_ЭМ – электромеханическая постоянная времени; К_Д – коэффициент передачи двигателя по управляющему воздействию.

Расчёт передаточной функции генератора.

Исходные данные:

; ; ; ; ; ;

; ; ; ; .

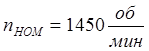Нагрузку считаем активной, индуктивностью об­мотки якоря пренебрегаем. Начальный поток возбуждения полагаем но­минальным, внутреннее сопротивление источника возбуждения не учи­тываем.

Находим конструктивную постоянную:

,

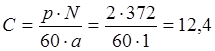откуда

.

Найдём значения r_Я.Ц.Г.:

.

Номинальный поток возбуждения рассчитываем по формуле:

.

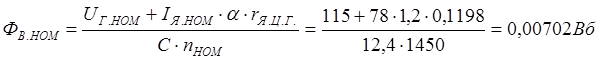где α = 1,2 – коэффициент, учитывающий перегрев обмотки по срав­нению с температурой 15 °С.

Определяем номинальный ток возбуждения и МДС на полюсе:

,

.

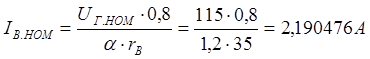Используя найденные значения Ф_В.НОМ и F_HОM, получаем масштабные коэффициенты по осям универсальной кривой намагничивания (рисунок 2):

, .

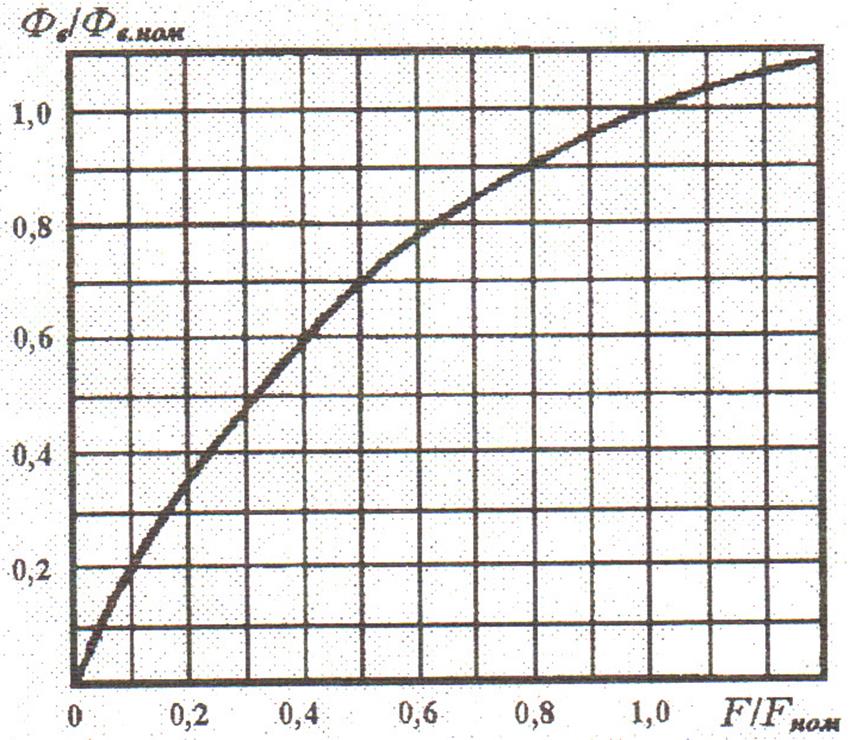
Рисунок 2 – Универсальная кривая намагничивания генераторов постоянного тока серии П

По кривой намагничивания при Ф_В = Ф_В.НОМ находим:

.

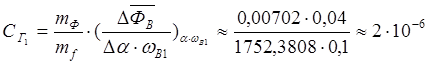Принимая σ_Г = 1,2 – коэффициент, учитывающий рас­сеяние магнитного потока ге­нератора (σ_Г = 1,15 – 1,2), определим индуктивность цепи возбуждения L_В: