Расчёт системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=1500 об/мин, p=6 кВт), страница 5

Строим график зависимости Р(ω) (рисунок 5).

Рисунок 5 – Вещественная частотная характеристика системы

При построении переходного процесса важно помнить свойства ВЧХ , а именно, что:

.

К полученной ВЧХ замкнутой системы применяют правила раз­бивки на трапеции, определяют параметры трапеций и представляют их в виде таблицы. При разбивке ВЧХ следует помнить, что все трапеции одной стороной должны прилегать к оси ординат, а также что должно выполняться равенство:

,

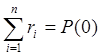где r_i – высота i-й трапеции; Р(0) – значение Р(ω) при ω = 0.

Коэффициент наклона рассчитывают по формуле:

,

где ω_с — частота среза, ω_d — динамическая частота.

Переход от табличной величины функции h(τ) к реальному ее значению h(t) производят по формуле:

,

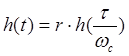где r — высота трапеции; t — реальное время, с, t = τ/ω_с; τ – табличное значение времени, с; ω_с - частота среза реальной трапеции.

Разбиваем ВЧХ на трапеции (рисунок 6).

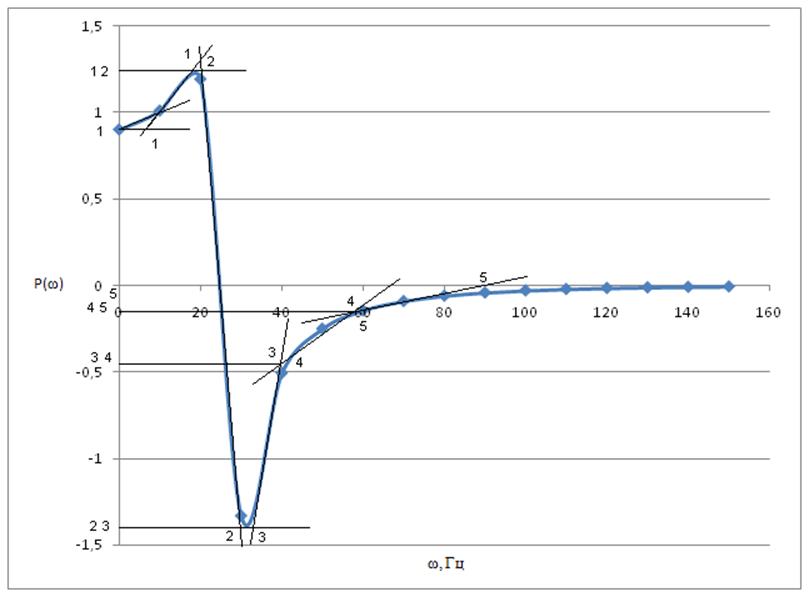
Рисунок 6 – Вещественная частотная характеристика системы, разбитая на трапеции

Составляем уравнения трапеций:

.

Таблица 3 – Параметры трапеций

Таблица 4 – h–функция