Другие предметы \ Судовые энергетические установки

Вибрация и шум судовых механизмов, страница 18

Задача расчета виброизоляции сводится, в основном, к следующему: для того, чтобы обезопасить амортизированный механизм от интенсивных вибраций (резонансные колебания), необходимо выбрать такие параметры виброизоляции, чтобы ни одна из 6 частот свободных колебаний механизма не совпала с зонами частот вынужденных колебаний . Иначе говоря, нужно добиться, чтобы все частоты были размещены в «окне» между зонами частот . Для этого строится частотный спектр вынужденных колебаний, который в общем случае может иметь вид, представленный на рис.8.15. На рисунке обозначены: а – зона частот колебаний от качки корабля; б – зона частот I-го порядка; в – зона частот 2-го порядка; г – зона частот колебаний от действия гидродинамических сил; д – зона частот колебаний от действия опрокидывающих моментов; , – минимальная и максимальная эксплуатационная угловая скорость вращения вала; – основной главный порядок гармоники опрокидывающих моментов дизеля.

В тех случаях, когда не удается выполнить это условие, желательно, чтобы частоты свободных колебаний лежали в области малых ходов, где ходовая вибрация развита слабее, так как силы, вызывающие вибрацию корпуса, пропорциональны квадрату числа оборотов, а для неуравновешенных механизмов, где влияние собственных возмущающих сил обычно сильнее влияния ходовой вибрации – вне зон частот возмущающих сил. Сказанное относится также к случаю, когда зоны ходовой вибрации смыкаются, не образуя «окон». Главным образом не должно допускаться совпадение с фиксированными оборотами главных машин на основных режимах их работы, соответствующих малому, среднему и полному ходам. Задача расчета несколько облегчается тем, что колебания совершаются в разных плоскостях.

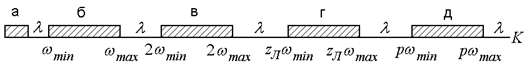
Рис. 8.15. Спектр частот возбудителей вибрации (вынужденных колебаний) на судне

Так, например, вынужденные колебания от неуравновешенных сил инерции и их моментов как I-го, так и 2-го порядка (зоны б и в) происходит в вертикальной плоскости, следовательно, на этих зонах можно размещать частоты свободных колебаний, происходящие в других плоскостях; вынужденные колебания зоны д происходят в плоскости шпангоутов судна, следовательно, здесь могут размещаться частоты свободных колебаний в других плоскостях.

Расчет частот свободных колебаний. Для случая виброизоляции, представленного на рис. 8.12,е, выражения для 6-тичастот свободных колебаний легко определяются из независимых решений дифференциальных уравнений (8.3), они имеют вид (Гц):

; ; ;

; ; .

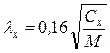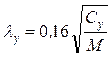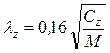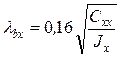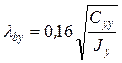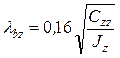Для случая виброизоляции, представленного на рис. 8.12,ж, выражения для 6-ти частот свободных колебаний имеют вид:

; ;

;

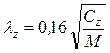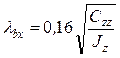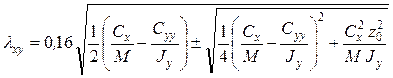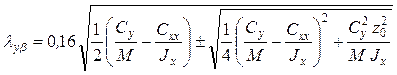Здесь – частоты свободных двухсвязных колебаний в плоскости , состоящих из поступательных перемещений вдоль оси и поворотных вокруг оси с частотами и , соответственно (в одном из них преобладают поступательные перемещения, в другом – поворотные); – частоты свободных двухсвязных колебаний в плоскости , состоящих из поступательных перемещений вдоль оси и поворотных округ оси с частотами и , соответственно (в одном из них преобладают поступательные перемещения, в другом – поворотные); – масса механизма, кг; , , – жесткости виброизоляции в направлении поступательных перемещений по осям , , , Н/м. Для случая виброизоляторов с одинаковой жесткостью

; ; ,

где – число виброизоляторов, а , , – значения их жесткостей в направлении соответствующих осей (указаны в характеристике каждого типоразмера виброизолятора, см., например, табл.8.6÷8.8); , , – жесткости виброизоляции относительно угловых перемещений вокруг осей , , , т.е. поворотные жесткости, Н/м. Эти жесткости в случае, если механизм поставлен, например, на 4-е одинаковых виброизолятора, (рис. 8.16), ориентированных единообразно и симметрично относительно центра тяжести механизма, выражаются следующим образом: