При раздельном рассмотрении в составе общей динамической модели вышеперечисленных явлений значительно упрощается понимание физических процессов, происходящих в СДУ, их математическое описание, повышается точность результатов расчетов.
Специального акустического расчета для оценки эффекта звукоизолирующей виброизоляции по общему уровню шума пока не применяют. Обычно исходят из бесспорного положения, что чем «мягче» виброизолятор, т.е. чем ниже частоты свободных колебаний механизма, тем лучше звукоизоляция. Критерием жесткости виброизоляции можно выбрать наиболее просто определяющуюся частоту свободных вертикальных колебании механизма.
Подобный расчет, не представляющий сложности, но обеспечивающий нужную величину звукоизоляции, является основным для механизмов, устанавливаемых на виброизоляторы. Этот расчет включает в себя проверку допустимой нагрузки на виброизолятор и на устойчивость механизма при качке (дифференте и крене).
Помимо этого расчета виброизоляция проверяется на отсутствие резонанса собственной частоты амортизированного механизма с частотой вынужденных колебаний от ходовой вибрации и неуравновешенных сил механизма. Этот расчет является значительно более сложным.
В общем случае амортизированный механизм совершает свободные (собственные) и вынужденные колебания, вызываемые возмущающими силами. Рассмотрим кратко эти колебания.
В каждой точке ![]() твердого тела
существуют три взаимно перпендикулярные оси
твердого тела
существуют три взаимно перпендикулярные оси ![]() ,
, ![]() ,
, ![]() ,
обладающие тем свойством, что центробежные моменты инерции тела относительно
этих осей равны нулю. Эти оси называются главными осями инерции в точке
,
обладающие тем свойством, что центробежные моменты инерции тела относительно
этих осей равны нулю. Эти оси называются главными осями инерции в точке ![]() .
.
Главные оси инерции тела, соответствующие его центру тяжести, называются главными центральными осями инерции.
Амортизированный механизм можно рассматривать как твердое
тело, упруго соединенное с неподвижным основанием (фундаментом) бесконечной
массы и жесткости. Тогда положение тела при малых перемещениях по отношению к неподвижному основанию определяется тремя перемещениями ![]() ,
,
![]() ,
, ![]() по
отношению к его неподвижному центру тяжести в направлении неподвижных осей
(рис. 8.14)
по
отношению к его неподвижному центру тяжести в направлении неподвижных осей
(рис. 8.14) ![]() ,
, ![]() ,
, ![]() и тремя вращательными перемещениями
и тремя вращательными перемещениями ![]() ,
, ![]() ,
, ![]() вокруг этих осей, т.е. амортизированное
тело будет иметь в общем случае шесть степеней свободы.
вокруг этих осей, т.е. амортизированное
тело будет иметь в общем случае шесть степеней свободы.
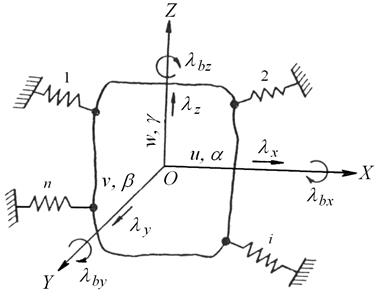
Рис. 8.14. Схема амортизированного механизма в общем случае
Таким образом, задача о свободных колебаниях амортизированного
механизма в общем случае сводится к определению шести частот свободных
колебаний ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и может
быть решена, если известны масса механизма, моменты инерции его относительно
главных осей инерции и жесткости виброизоляторов, соединяющих механизм с
фундаментами. Если оси
и может
быть решена, если известны масса механизма, моменты инерции его относительно
главных осей инерции и жесткости виброизоляторов, соединяющих механизм с
фундаментами. Если оси ![]() ,
, ![]() и
и ![]() совпадают
с главными центральными осями инерции амортизированного механизма, а жесткость
каждого виброизолятора представить в виде суммы трех составляющих, направленных
параллельно выбранным координатным осям, то задача о движении такого тела
решается следующим образом.
совпадают
с главными центральными осями инерции амортизированного механизма, а жесткость
каждого виброизолятора представить в виде суммы трех составляющих, направленных
параллельно выбранным координатным осям, то задача о движении такого тела
решается следующим образом.
Обозначим: ![]() ,
, ![]() ,
, ![]() –
составляющие реакции i-го виброизолятора по осям
–
составляющие реакции i-го виброизолятора по осям ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() – координаты точки крепления
– координаты точки крепления ![]() -го виброизолятора к механизму;
-го виброизолятора к механизму; ![]() ,
, ![]() ,
, ![]() – перемещения этой точки в
направлении осей
– перемещения этой точки в
направлении осей ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() –
составляющие линейной жесткости
–
составляющие линейной жесткости ![]() -го виброизолятора в
направлении осей
-го виброизолятора в
направлении осей ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() –
углы поворота вокруг осей
–
углы поворота вокруг осей ![]() ,
, ![]() ,
, ![]() ; при
этом углы будут положительными, если ось
; при
этом углы будут положительными, если ось ![]() переходит
кратчайшим путем в положение, занимаемое осью
переходит
кратчайшим путем в положение, занимаемое осью ![]() и
т.д.;
и
т.д.; ![]() ,
, ![]() ,
, ![]() – соответствующие этим вращениям
реактивные моменты i-го виброизолятора, приведенные к
точке крепления этого виброизолятора к механизму;
– соответствующие этим вращениям
реактивные моменты i-го виброизолятора, приведенные к
точке крепления этого виброизолятора к механизму; ![]() ,
, ![]() ,
, ![]() –
жесткости виброизолятора, соответствующие этим моментам;
–
жесткости виброизолятора, соответствующие этим моментам; ![]() ,
, ![]() ,
, ![]() – перемещения центра тяжести
амортизированного механизма в направлении осей
– перемещения центра тяжести
амортизированного механизма в направлении осей ![]() ,
, ![]() ,
, ![]() .
.
Из принятых обозначений непосредственно следует, что
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]() .
.
Кроме того, между перемещениями точки крепления виброизолятора к механизму и перемещениями последнего существуют зависимости:
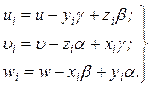
Движение амортизированного тела описывают следующие уравнения:
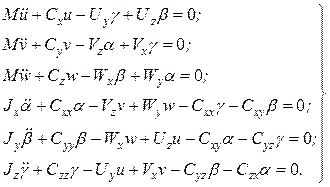 (8.2)
(8.2)
В них: ![]() – масса тела;
– масса тела; 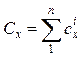 ;
; 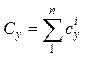 ;
; 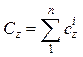 ;
; 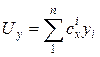 ;
; 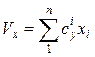 ;
; 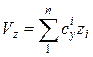 ;
; 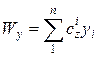 ;
; 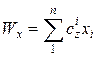 ;
; 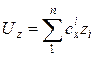 ;
; 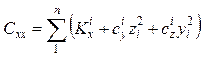 ;
; 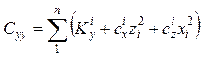 ;
;  ;
;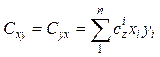 ;
;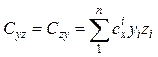 ;
; 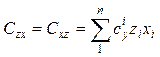 ;
; ![]() ,
, ![]() ,
, ![]() – полярные моменты инерции тела
относительно осей
– полярные моменты инерции тела
относительно осей ![]() ,
, ![]() ,
, ![]() соответственно.
соответственно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.