Вибрация и шум судовых механизмов, страница 17

- вращательные колебания относительно оси

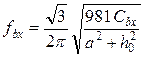                                         ,                                (8.7)

где  – вес виброизолируемого агрегата.

Анализ формул (8.5)÷(8.7) показывает, что все собственные колебания определяются через вертикальные колебания двигателя , установленного на наклонные виброизоляторы, при помощи простых уравнений:

,  ,  ,

где 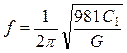 – частота вертикальных колебаний двигателя, установленного на наклонные опоры;

; ; .

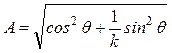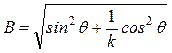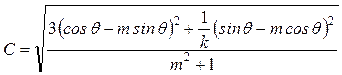Здесь  определяется по формуле (8.4).

При наклонных опорах статический прогиб равен

.

Наклонные опоры позволяют разделить колебания только в плоскости , в плоскости  колебания будут двухсвязанными, и собственные частоты колебания определяются как для двухсвязанных колебаний опор, но жесткости в отличие от ненаклонного крепления находятся по следующим выражениям:

- жесткость сдвига по оси

;

- жесткость при вращательных колебаниях относительно оси

,

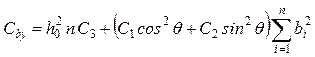где  – сумма квадратов плеч всех виброизоляторов по оси .

Величина вертикальной жесткости относительно вертикальной оси определяется по формуле

,

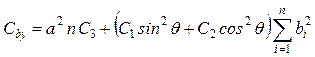где  – сумма квадратов плеч всех виброизоляторов в направлении осей  и .

Однако в большинстве случаев для многоцилиндровых однорядных двигателей надобность определения частот последних трех колебаний отпадает в виду уравновешенности двигателей и отсутствия усилий, действующих в этих направлениях.

Часто из конструктивных соображений задаются значением , тогда при известной величине  определяются необходимые жесткости виброизоляторов, или при известных жесткостях определяется оптимальная высота установки опор по отношению к центру тяжести двигателя.

8.3.3.2. Вынужденные колебания виброизоляторного                                                        механизма

К возмущающим силам, вызывающим вынужденные колебания, происходящие с частотой возмущающей силы, относятся: качка корабля, ходовая вибрация и импульсы, возникающие в работающем механизме. Для случая, если качка корабля постоянна, круговая частота вынужденных колебаний  будет равна частоте кажущегося бега волны и может быть определена из формулы (Гц)

,

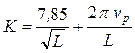где  – длина волны, м;  – скорость судна, м/с.

Эти частоты малы, а при следовании судна лагом к волне еще меньше, так как в этом случае второй член правой части может быть принят равным нулю и  = 1÷2 Гц.

Ходовую вибрацию и импульсы в работающем механизме вызывают следующие причины.

а) Неуравновешенность валопровода и винта. Вибрация вследствие этой причины может быть весьма интенсивной, она имеет частоту первого порядка, т.е. порядка числа оборотов вала

 Гц,

где  – число оборотов вала в минуту.

б) Гидродинамические силы, развивающиеся при работе гребных винтов и обусловленные неравномерным подходом струи к лопасти винта.

Частота этой вибрации кратна произведению из числа лопастей винта на число оборотов вала

 Гц,

где  – число лопастей.

в) Силы инерции и моменты неуравновешенных вращающихся и поступательно движущихся масс двигателей и механизмов. Вибрации, вызываемые этими силами и моментами, имеют частоту I-го порядка для сил и моментов I-го порядка и в два раза больше, т.е. частоту 2-го порядка для сил и моментов 2-го порядка

 Гц,

 Гц.

г) Главная гармоника опрокидывающего момента дизелей. Порядок этой гармоники кратен числу цилиндров для двухтактных дизелей и половине этого числа для четырехтактных дизелей

 Гц,

 – основной главный порядок гармоники опрокидывающих моментов.

Вынужденные колебания, вызываемые импульсами в работающих роторных двигателях, имеют весьма высокие частоты. Так например, частота вибраций статора электродвигателя

 Гц,

где  – число пазов якоря.

Диапазон частот того или иного порядка определяется диапазоном рабочих частот вращения от  до  (÷).

8.3.3.3. Расчет виброизоляции