В общем случае, когда все коэффициенты жесткости ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() не равны нулю, переменные
не равны нулю, переменные ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() в
уравнениях (8.2) не разделяются, и каждое из шести перемещений в той, или иной
мере неотделимо от остальных пяти перемещений (многосвязные колебания).
Определение их требует совместного решения системы (8.2), что представляет
значительные трудности. Кроме этого следует отметить, что такая виброизоляция,
где все перемещения связаны между собой, практически не применяется.
в
уравнениях (8.2) не разделяются, и каждое из шести перемещений в той, или иной
мере неотделимо от остальных пяти перемещений (многосвязные колебания).
Определение их требует совместного решения системы (8.2), что представляет
значительные трудности. Кроме этого следует отметить, что такая виброизоляция,
где все перемещения связаны между собой, практически не применяется.
Для рассмотрения частных случаев, имеющих место в практике виброизоляции, воспользуемся понятием “центр жесткости виброизоляции”.
Если распространить положение механики для систем материальных точек на систему виброизоляторов, то под центром жесткости виброизоляции будем подразумевать (если только таковой у рассматриваемой системы имеется) точку, по отношению к которой главный момент реакции виброизоляторов равен нулю при любых поступательных перемещениях амортизированного тела, т.е. точку, в которой можно считать сосредоточенной общую жесткость упругого основания.
Наиболее существенные случаи виброизоляции, характерные в отношении способов определения частот свободных колебаний, представлены на рис. 8.12.
Наиболее простой случай (см. рис. 8.12,е), когда центр тяжести механизма совпадает с центром жесткости виброизоляции, а главные оси инерции механизма совпадают с осями жесткости виброизоляции.
В этом случае главные моменты реакций виброизоляторов, отнесенные
к осям ![]() ,
, ![]() ,
, ![]() равны нулю, и коэффициенты жесткости,
зависящие от произведения переменных, тоже равны нулю, и уравнения (8.2)
принимают наиболее простой вид
равны нулю, и коэффициенты жесткости,
зависящие от произведения переменных, тоже равны нулю, и уравнения (8.2)
принимают наиболее простой вид
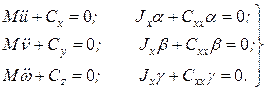 (8.3)
(8.3)
В этом случае все шесть движений, соответствующих перемещениям
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
оказываются независимыми, т.е. имеем односвязные колебания.
,
оказываются независимыми, т.е. имеем односвязные колебания.
Наиболее распространенным случаем является случай (см. рис.8.12,ж), когда центр тяжести механизма не совпадает с центром жесткости виброизоляции, все главные центральные оси инерции механизма являются одновременно главными, но нецентральными осями жесткости виброизоляции.
При этом центр жесткости виброизоляции лежит на одной из
главных осей инерции механизма. Приняв за эту ось вертикальную ось ![]() , уравнения (8.3) примут вид:
, уравнения (8.3) примут вид:
- двухсвязные колебания
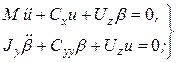
- двухсвязные колебания
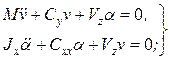
- односвязные колебания
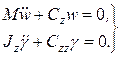
В этом случае описываются два односвязных колебания (вдоль
и вокруг оси ![]() ) и две группы двухсвязных
колебаний, в одной из которых
) и две группы двухсвязных
колебаний, в одной из которых ![]() связано с
связано с ![]() , в другой
, в другой ![]() связано
с
связано
с ![]() .
.
Установка двигателей на наклонные выброизоляторы (рис.8.12,г) имеет много преимуществ по сравнению с установкой на ненаклонные виброизоляторы [29]. С помощью наклонных виброизоляторов можно осуществить так называемый «метод динамической подвески двигателя», позволяющий разделить колебания, т.е. сделать их независимыми одно от другого, и тем самым облегчить их расчет.
Расчет собственных колебаний сводится к следующему.
Определяется центр тяжести двигателя, а сам двигатель представляется как параллелепипед с равномерным распределением массы, вследствие чего расчет значительно упрощается.
Зная величины суммарных жесткостей на сжатие ![]() и на сдвиг в двух направлениях
и на сдвиг в двух направлениях ![]() и
и ![]() , где
, где ![]() ,
, ![]() ,
, ![]() – жесткости одного виброизолятора (из
– жесткости одного виброизолятора (из ![]() установленных) в направлении трех его
главных упругих осей, и величины отношения жесткостей
установленных) в направлении трех его
главных упругих осей, и величины отношения жесткостей
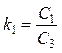 ,
, 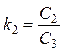 ,
, 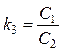 ,
,
найдем условие разделения собственных колебаний системы
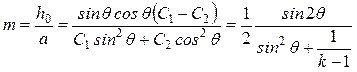 , (8.4)
, (8.4)
где ![]() – угол наклона опор к
вертикальной оси.
– угол наклона опор к
вертикальной оси.
При такой величине отношения ![]() наклонные
опоры обеспечат разделение колебания в плоскости
наклонные
опоры обеспечат разделение колебания в плоскости ![]() , в
которой действует опрокидывающий момент и происходит обычно наибольшая вибрация
двигателя. При этом суммарные жесткости виброизоляторов в плоскости
, в
которой действует опрокидывающий момент и происходит обычно наибольшая вибрация
двигателя. При этом суммарные жесткости виброизоляторов в плоскости ![]() , соответствующие частотам поступательных колебаний
двигателя вдоль оси
, соответствующие частотам поступательных колебаний
двигателя вдоль оси ![]() , определяются по следующим
формулам
, определяются по следующим
формулам
![]() ,
,
![]() ,
,
а вращательная жесткость
![]() .
.
Тогда частоты собственных колебаний будут равны:
- вертикальные колебания
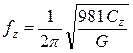 ; (8.5)
; (8.5)
- горизонтальные колебания
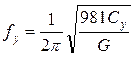 ; (8.6)
; (8.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.