Структура и режимы течения в неизобарических сверхзвуковых струях, страница 9

Для случая сильного взаимодействия между частицами и газо­вой фазой, имеющего место в струях с высокой плотностью и незна­чительной неизобаричностью, используется другое приближение, при котором наличие частиц в струе учитывается введением эффективного показателя адиабаты, и их совокупность представляется в виде некоторого «псевдогаза».

На практике часто возникают задачи, связанные с определением структуры струй, истекающих из устройств с неосесимметричной конфигурацией, например, струй, истекающих из компоновки 5-ти близко расположенных сопл. Здесь существенным фактором является взаимодействие струй между собой, приводящее к отличиям их свойств от свойств, соответствующих истечению из одиночного сопла. В общем случае структура течения в такой системе струй довольно сложна, а ее математический расчет в точной постановке затруднителен. Поэтому здесь важны накопление и обобщение экспериментальных данных. В качестве примера успешной реализации такого подхода можно отметить следующее обобщение, сделанное для истечения при сильном недорасширении (n > 10) из нескольких близко расположенных (на расстоянии порядка нескольких r_а) сопел. Установлено, что, несмотря на наличие вблизи срезов сопел сложной системы интерференционных ударных волн, образуется «суммарная» бочкообразная структура, которая по конфигурации и своим свойствам напоминает бочкообразную структуру начального участка струи, истекающей из одиночного сопла. Характерные размеры этой структуры могут быть приближенно определены по соотношениям для одиночной струи, истекающей из некоторого эквивалентного одиночного сопла с расходом и потоками импульса и энергии, равными сумме этих величин для всех сопл данной компоновки.

14.2. Граница слоя смешения дозвуковой струи.

Рассмотрим вопрос о расширении границ турбулентной струи. Предположим, что скорость нарастания толщины пограничного слоя b пропорциональна пульсационной составляющей поперечной скорости

                                                          

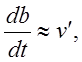
которая пропорциональна поперечному градиенту продольной скорости потока

                                                             

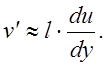
Здесь l- путь турбулентного смешения. Ввиду подобия профилей скорости в различных сечениях слоя смешения струи поперечный градиент продольной скорости пропорционален разности скоростей на границах

                                                  

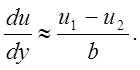
Вследствие этого имеем

                                                   .

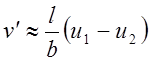Из подобия профилей скорости следует, что l/b = const. Поэтому

                                                  

Отсюда

                                                    

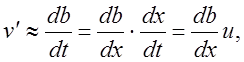
и закон нарастания толщины слоя смешения по длине струи можно представить в следующем виде:

                                                  

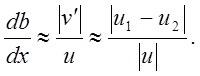
Величина v'/u называется степенью турбулентности потока, она всегда положительна и, следовательно, db/dx>0. Величина u может быть оценена для несжимаемой жидкости как

                                                  

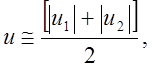
Тогда

                                                  

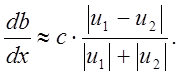
Для постоянных по длине значений скорости на границах величина в правой части выражения является постоянной. Следовательно, и db/dx=const. В случае u₂ = 0 можно получить зависимость толщины от координаты вдоль струи b₃ = cx. Тогда в общем случае толщина струи определяется как

                              

причем знак минус берется при u₁>u₂. Следовательно, если внешний поток (скорость u₂) является спутным струе, то это уменьшает угол расширения границ струи и он доходит до нуля при равенстве скоростей потока и струи. Если поток встречный, то угол расширения струи остается постоянным и равным углу при истечении струи в неподвижное затопленное пространство, хотя это и звучит несколько парадоксально. Экспериментально показано, что для холодной струи (комнатная температура) воздуха угол расширения составляет @ 6°. Угол расширения сверхзвуковых струй не намного отличается от этого значения.

15. ШУМ СТРУЙ