Структура и режимы течения в неизобарических сверхзвуковых струях, страница 5

получаем

.

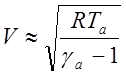Учитывая, что для М_а >>1

,

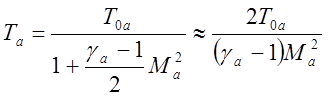получаем, что характерный полярный угол течения q будет определяться отношением

                                       (14.4)

Из соотношения видно, что с ростом числа Маха сопла угол раскрытия струи уменьшается и длина первой ячейки волновой структуры струи увеличивается. Условия U = const и q < 1 позволяют применить для приближенного описания течения метод нестационарной аналогии (закон плоских сечений). Метод основан на том, что при переходе в систему координат, движущуюся со скоростью U, течение в струе выглядит как радиальное сверхзвуковое расширение из точки. Сейчас же достаточно указать, что, используя в соответствии с этим методом связь продольной координаты х со временем t по соотношениям x=Ut и dx=Udt, можно следующим образом определить размеры Х и Y.

Выделим в поперечном сечении струи плоский слой (рис.48) газа, толщиной dx, масса газа прошедшего через сопло за время dt, равна G_adt. Считается, что тепловая энергия e_aG_adt этого газа целиком расходуется на работупопреодолению давления газа затопленного пространства и определяется соотношением

После замены в последнем соотношении dt на dx/U находим

,                                          (14.5)

где r_а - радиус выходного сечения сопла. Так как расход G_a можно определить как , по определению степени нерасчетности 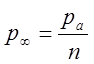. Тепловую энергию e_a, с использованием (14.3), можно определить как 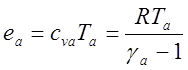. Используя уравнение состояния идеального газа 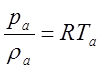 получаем

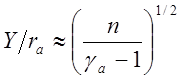                                            (14.6.)

Из соотношения видно, что с ростом степени нерасчетности струи диаметр круглой струи возрастает как корень из нерасчетности и, например, струя углекислого газа (g_а = 1,33) будет большего диаметра, чем струя гелия (g_а = 1,6). Для продольного размера струи с использованием (14.4) и (14.6) получаем

Из соотношения видно, что с ростом числа Маха сопла и степени нерасчетности струи первая ячейка волновой структуры недорасширенной струи удлиняется. Комплекс  является параметром подобия геометрии первой ячейки струи, как недорасширенной, так и перерасширенной.

Диапазон изменения параметра п в практических задачах очень велик - от 10^- 1 до 10¹⁰. Поэтому изменения Х и Y при изменении п значительны. Экспериментальными и расчетными исследованиями установлено, что Х и Y пропорциональны  в очень широких пределах для сильно недорасширенных струй (при п > 3).

При истечении в спутный сверхзвуковой поток при М_¥>2 давление вдоль границы струи существенно переменное, а на начальном участке сильно недорасширенной струи оно пропорционально импульсу внешнего потока

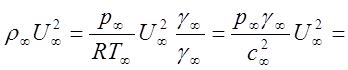p_¥g_¥М_¥²,

что приводит к следующим зависимостям размеров Х и У от безразмерных критериев

,

а для qсохраняется прежняя оценка (14.4). Здесь сказывается уменьшение диаметра струи из-за увеличения противодавления внешней среды, которое слабо сказывается на длину самой струи.

Систематические расчеты по теории невязкой жидкости позволили провести детальное исследование влияния параметров п, у_а, М_а, g_а, М_¥ на структуру струи. Анализ результатов этих расчетов устанавливает для начального участка недорасширенной струи автомодельность его геометрической формы (ударные волны, границу) и распределения параметров в координатах подобия х/Х и y/Y, также выявляет гиперзвуковой параметр подобия К = М_¥q ~ М_¥Y/X ~ М_¥/М_а. При слабом влиянии эффектов вязкости (большие числа Рейнольдса при ламинарном течении и близость к единице параметра спутности т при турбулентном течении) установленный принцип автомодельности может быть сформулирован в виде следующего правила: при одинаковых значениях гиперзвукового пирометра подобия К в сходственных сечениях (x/Х = const) поля распределения параметров подобны по нормированной координате подобия y/Y.