Структура и режимы течения в неизобарических сверхзвуковых струях, страница 14

Внося последовательно производные по координате х под интеграл аналогично п. 15.1.4 получим под интегралом три члена, из которых на большом расстоянии будет не мал только первый член со второй производной по времени и дифференцированием по координате х_ij только второго аргумента в тензоре. Учитывая, что производная по координате х_i от модуля вектора  при постоянном x и с использованием (15.18) дает

                                         ,

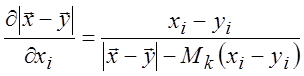то уравнение (15.19) можно преобразовать в уравнение

                   

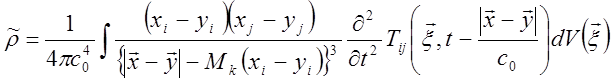
Вводя угол q между направлением на точку регистрации звука и направлением движения источника 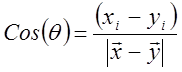, получим

                   

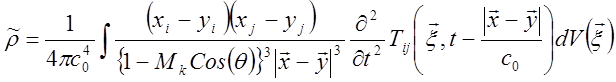
На больших расстояниях от источника  и запаздыванием по времени можно пренебречь. Тогда

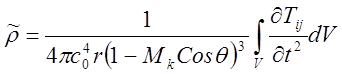                                                                           (15.20)

Интенсивность звука I определяется двумя последними сомножителями в соотношении (15.6). Подставляя в них (15.20) получаем

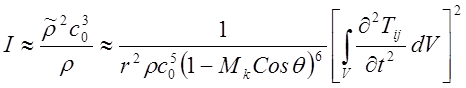                                                         (15.21)

Видно, что угловая индикатрисса интенсивности звука вытянута в направлении течения струи, так как знаменатель в (15.21) уменьшается при стремлении угла q к нулю. Однако, тот же эффект движения источников уменьшает число элементарных объемов дающих синфазный вклад в излучение звуковой волны на коэффициент . Поэтому общая зависимость интенсивности излучения звука струей будет только в пятой степени

                              

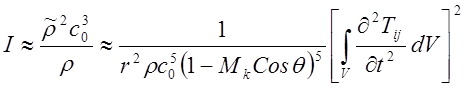
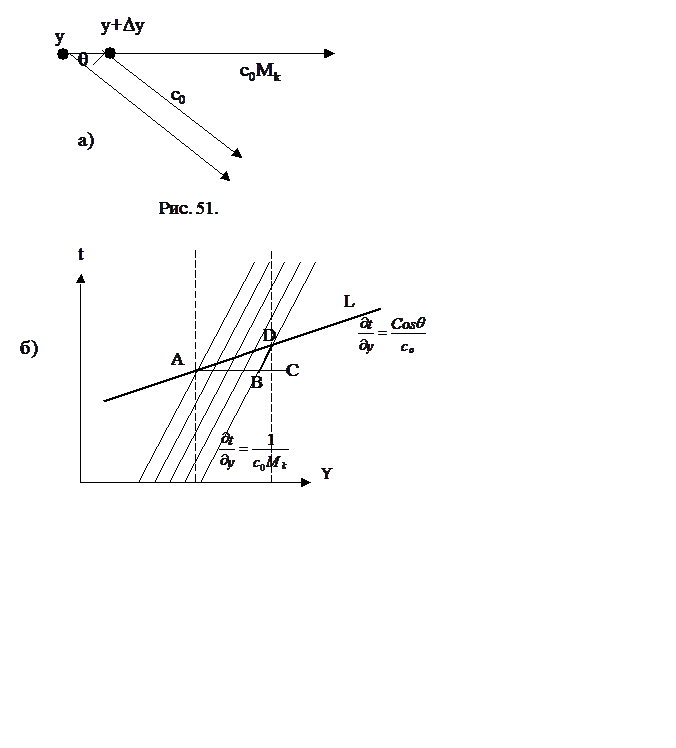Этот эффект можно пояснить графически. Если источник звука перемещается из точки y в точку y+Dy со скоростью с₀М_к, то для синфазного излучения звука в направлении под углом q к движению звук в точке y должен быть излучен на время Dt раньше (см. рис.51,а). Следовательно,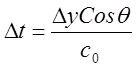 или в малых приращениях 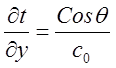. С другой стороны  или в малых приращениях 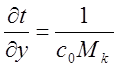. На графике рис. 51,б линией ADL показаны точки, из которых звук приходи в точку регистрации звука синфазно и усиливается. Серией наклонных линий показаны траектории движения протяженного источника звука, типа вихря. Неподвижный вихрь излучает звук из области AC, а при движении только из области AB. Отношение

                                                  

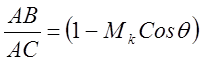
Следовательно, число источников сокращается на коэффициент (). В реальной струе на направленность влияет рефракция звука в неоднородном потоке струи, в том числе градиент скорости и градиент температуры в случае горячих струй. Наличие скорости и температуры в струе приводит к развороту фронтов звуковых волн в направлении перпендикулярном оси струи. Графически влияние разных факторов на направленность шума показано на рис. 52.

По аналогии с выводом члена для направленности квадрупольного шума можно легко показать, что направленность дипольного шума будет описываться зависимостью

          ,

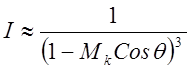так как при внесении производной по х под интеграл возникает только вторая степень обратной зависимости от угла, а направленность монопольного шума будет определяться только первой степенью, так как производная по координате х здесь не берется

                                                   .

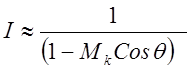Из соотношений видно, что они верны только для дозвуковых струй, когда число Маха конвекции М_к<1 и знаменатель не обращается в нуль.

15.1.6. Собственный и сдвиговый шум струи.

Все предыдущие рассуждения относились к турбулентному шуму струи, в которой нет градиента средней скорости. Этот шум называется собственным шумом турбулентной струи. При наличии такого градиента происходит дополнительная нестационарная деформация вихрей в слое смешения из-за разницы скоростей по объему вихря и его движения в области переменной средней скорости. При этом возникают пульсации давления вокруг вихря и создается дополнительный шум, так называемый сдвиговый шум. Его происхождение можно пояснить на простом примере, когда имеет место только квадрупольный шум струи потому, что он доминирует при больших скоростях, когда в струе велики поперечные градиенты средней скорости. Для большей простоты рассмотрим только квадрупольный шум струи. В тензоре T_ij пренебрежем вязкими членами и членом с теплопроводностью и рассмотрим турбулентные движения только вдоль струи по координате х. Пусть скорость жидкости состоит из суммы скорости среднего движения U и пульсаций u’. Тогда