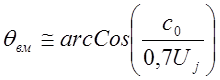Структура и режимы течения в неизобарических сверхзвуковых струях, страница 16

                                           ,

Здесь U_j – скорость газа на оси струи, которая зависит от степени нерасчетности струи n.

На этих скоростях соотношения (15.22) или (15.23) становятся неверными, так как при их выводе не учитывалось влияние сжимаемости газа и наличие времени запаздывания прихода звуковых волн от различных точек объема вихря. При числе Маха конвекции вихрей равном единице знаменатель в соотношениях обращается в ноль. При равенстве М_кCosq = 1, звуковая волна движется к приемнику со скоростью звука и проекция скорости источника на направление к приемнику тоже равна скорости звук. В следствие этого не существует направлений, при которых волны могут догонать друг друга и суммироваться. Это приводит к тому, что с точки зрения наблюдателя с приемником звука не существует движений в слое смешения и вихри в нем движутся как бы «замороженные», что формально соответствует вышеупомянутым маленьким «снарядам» на границе струи, которые при своем сверхзвуковом движении генерируют наклонные волны. Это приводит к тому, что мощность излучения звука в этих условиях становится пропорциональной только энергии струи

                                                                                               (15.24)

В свою очередь, на сверхзвуковых скоростях турбулентный шум также модифицируется. В частности, было показано, что направленность квадрупольного турбулентного шума описывается фактором 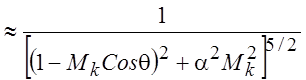, где 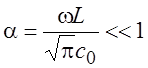. Здесь 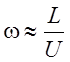 - характерная частота пульсаций скорости в слое смешения, а  - характерный размер вихря. Введение слагаемого в знаменатель устраняет обращение знаменателя в ноль и обращение мощности звука в бесконечность. Видно, что максимум излучения совпадает с направлением по соотношению для угла q_ув..

15.2.2. Ударно-волновой шум

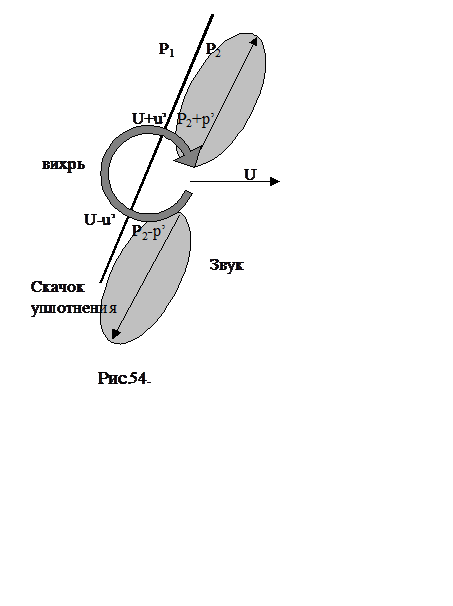
Этот тип шума характерен только для нерасчетных сверхзвуковых струй, в которых имеется волновая структура (система скачков уплотнения). Турбулентные вихри в слое смешения со сверхзвуковой скоростью взаимодействуют со скачками уплотнения, выходящими в слой смешения. При прохождении вихря через скачок генерируется ударно-волновой шум. Механизм генерации этого звука проиллюстрирован схемой на рис.54. При пересечении вихрем с эффективной круговой скоростью u’ линии скачка уплотнения в одной части вихря давление за скачком повышается на величину p’, а в другой уменьшается на туже величину. Возникает две волны: давления и разрежения, расходящиеся в противоположных направлениях, так как вдоль оси симметрии (вдоль направления движения вихря) они гасят друг друга. Система ведет себя как дипольный источник с направлением излучения вдоль скачка уплотнения. Очевидно, что мощность излучения ударно-волнового шума будет также связана с полной энергией струи, так как интенсивность генерации звука при прохождении возмущений скорости через скачок не должна зависеть от мультипольности турбулентных движений. Поэтому

В нерасчетной струе с большим числом ячеек волновой структуры вихри создают импульсы акустического давления на каждом скачке уплотнения, пересекающем слой смешения, как движущаяся палочка по стиральной доске. Отсюда легко определить частоту ударно-волнового шума струи.

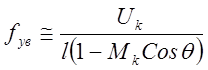                                                (15.25)

Здесь l – длина ячеек волновой структуры струи; U_k – скорость конвекции вихрей в слое смешения (U_k @ 0,7U_j для сверхзвуковых струй), М_к – число Маха конвекции вихрей по отношению к скорости звука во внешнем пространстве с₀. Отношение скорости конвекции к длине ячейки дает частоту в системе координат, движущейся со скоростью конвекции вихрей. Член в скобках учитывает допплеровкий сдвиг частоты в лабораторной системе координат. Направленность ударно-волнового шума почти изотропна из-за дифракции звука на конце линии скачка, когда он пересекает звуковую линию в слое смешения. Из соотношения (15.25) видно, что частота звука повышается в направлении движения струи и понижается вверх по потоку. Этот тип шума конкурирует по интенсивности с шумом маховских волн и турбулентным шумом основного участка струи и генерируется на всей длине сверхзвукового участка струи.