Структура и режимы течения в неизобарических сверхзвуковых струях, страница 12

К аэродинамическим источникам звука преимущественно монопольного характера можно отнести: выхлоп поршневых двигателей, воздушные сирены, кавитационные явления в жидкостях, шум закипающей воды, шум газовых горелок, горячих дозвуковых струй и факела ракетных двигателей. Это связано с радиальными колебаниями элементарных объемов в потоке под воздействием точечных пульсаций давления или нагревания и охлаждения объемов. Схема движений в монополе и диаграмма направленности звука приведена на рис. 48. Как видно из рисунка диаграмма направленности излучения монополя изотропна.

15.1.3. Излучение звука диполями

Оставим теперь в правой части уравнения (15.4) только второй член с F_i ответственный за изменение массовых сил. Тогда решение волнового уравнения (15.4) будет

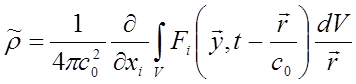                                                                 (15.9)

Как и ранее будем рассматривать длинноволновое приближение, когда задержкой времени и, следовательно, членом  в аргументах функции F_i можно пренебречь. Внесем производную по координате х под интеграл и продифференцируем подинтегральное выражение

                    

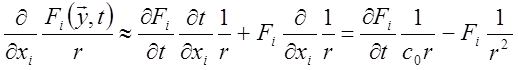
На больших расстояниях от источника звука второй член в правой части соотношения становится значительно меньше первого. Тогда соотношение (15.9) можно преобразовать к виду

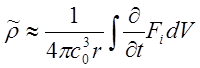                                                                                               (15.10)

или в виде соотношения для порядков для производной по времени и оценки величины F_i из (15.2) получаем

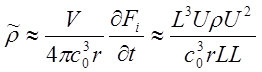                                                                                      (15.11)

Подставляя выражение (15.11) в соотношение (15.6) получаем зависимость для мощности дипольного источника шума потока

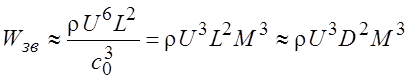                                             (15.12)

Из соотношения видно, что мощность пропорциональна суммарной энергии потока (первые три сомножителя) и числу Маха в третьей степени. Следовательно, с ростом скорости потока интенсивность дипольных источников растет быстрее монопольных. Эту зависимость иногда называют «законом шестой степени» от скорости.

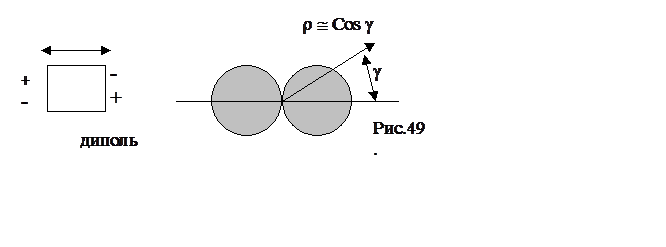Модель диполя можно представить в виде тела пульсирующего вдоль выделенной оси. Схема движений в диполе и диаграмма направленности приведена на рис. 49. Как видно из рисунка диаграмма направленности имеет два максимума и минимум на оси симметрии колебаний объема. Вдоль оси симметрии пульсации плотности, приходящие с правой и левой грани, равны по величине и противоположны по знаку. Поэтому пульсации взаимно уничтожаются, образуя минимум интенсивности. Диполь можно представить также и в виде системы из двух монополей пульсирующих в противофазе по времени. Такая система также будет давать диаграмму направленности типа рис. 49.

К аэродинамическим источникам звука преимущественно дипольного характера можно отнести: вентиляторы, компрессоры, газовые турбины, воздушные винты, обтекаемые поверхности каналов и летательных аппаратов.

15.1.4. Излучение звука квадруполями

Оставим теперь в правой части уравнения (15.4) только третий, тензорный член. Тогда решением уравнения будет выражение

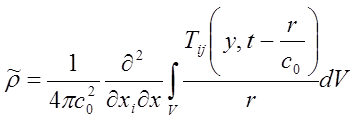                                                      (15.13)

Здесь, также как и для случая монополя и диполя, выражение (13.13) описывает суммарные возмущения плотности, порождаемые взаимодействием турбулентных вихрей (первый член тензора T_ij) и вязкими напряжениями в турбулентном потоке (второй член этого тензора) в элементарных объемах dV общего объема области генерации звука V на расстоянии r от него. В предположении низкочастотных волн и, пренебрегая задержкой сигнала от различных точек объема, внесем последовательно производные по координате х под интеграл и продифференцируем подинтегральное выражение по аналогии со взятием производных в п.15.1.3. Тогда получим  выражение нового вида

                    

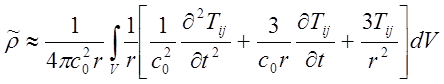
Для больших расстояний от источника звука второй и третий член под интегралом становятся много меньше первого и это выражение сворачивается к виду

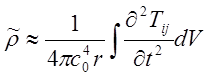                                        (15.14)