Структура и режимы течения в неизобарических сверхзвуковых струях, страница 11

Пусть в правой части уравнения (15.4) останется только расходный член с Q ответственный за изменение производительного источника шума. Решением его будет уравнение

                                 .

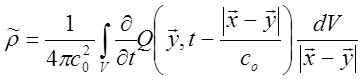Здесь  - переменная составляющая плотности; V – объем, занимаемый источником звука;  - вектор до некоторой точки в объеме источника звука и вектор до точки регистрации звука вне объема источника звука. Вектор () соединяет точку в объеме источника звука с точкой регистрации звука вне объема. Будем для простоты рассматривать звуковое поле на больших расстояниях от источника, когда расстояние до него много больше его характерного размера r>>L. Решением уравнения (15.4) в этом случае является соотношение для пульсаций плотности

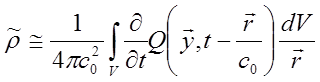.                                    (15.5)

Здесь - соответственно, координаты элемента в объеме источника и координата приемника звука на большом расстоянии вне источника. Уравнение (15.5) описывает суммарные пульсации плотности, порождаемые локальными источниками пульсаций расхода Q размера dV в объеме V на расстоянии r от этого объема. Член после запятой в скобках под интегралом описывает задержку во времени прихода возмущений плотности в точку измерения.

Так как механическая мощность любого процесса пропорциональна произведению силы на скорость, то для мощности излучаемого звука получаем

                                                                       

Здесь S – площадь поверхности вокруг источника звука, р_ак и u_ак – значения звукового давления и скорости газа в звуковой волне на границе поверхности. Используя соотношение для скорости воздуха в акустических пульсациях u_ак

                                                  

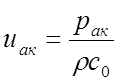
Здесь rс₀ – акустический импеданс среды или акустическое сопротивление, где r - средняя величина плотности и используя уравнение состояния  и выражение для скорости звука , получаем

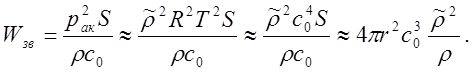                          (15.6)

Здесь площадь S выражена через расстояние до источника r. Здесь мы также неявно использовали предположение, что в звуковой волне температура меняется слабо и . Соотношение для u_ак вытекает их уравнения Бернулли при условии, что давление р_ак и скорость газа u_ак в звуковой волне значительно меньше статического давления воздуха р и скорости звука с₀, что и имеет место в действительности

                                 .

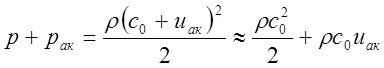Принимая во внимание только члены первого порядка малости получаем вышеупомянутое соотношение для u_ак.

Если рассматривать частоты колебаний, когда длина звуковой волны l много больше характерного размера L источника звука (вихря), т.е. l>>L, то роль задержки времени в соотношении (15.5) будет незначительна и соотношение (15.5) можно переписать в виде

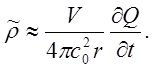                                                  (15.7)

Подставляя (15.7) в (15.6) получаем

                                                  

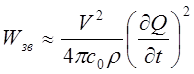
Вводя в задачу характерную частоту колебаний f, характерную скорость течения потока U и характерный размер источника звука L получаем для производной по времени 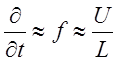. Из уравнения (15.1) тогда получаем оценку для расхода 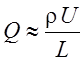 из размерности и первого и второго члена в левой части, а . Окончательно получаем

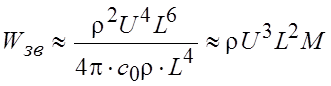                                                                            (15.8)

Известно, что характерный масштаб турбулентности пропорционален масштабу течения в целом. Поэтому величина турбулентных источников или вихрей L в струях будет пропорциональна диаметру сопла D, из которого истекает струя. Отсюда видно, что мощность дипольного источника в длинноволновом диапазоне, где по данным экспериментальных измерений всегда наблюдаются максимальные значения интенсивности звука, будет пропорциональна суммарному потоку энергии газа (rU³D²) и числу Маха М.

                                                   .

Следует заметить, что здесь под числом Маха подразумевается число Маха конвекции вихрей в слое смешения струи, а не число Маха на оси струи. Последнее примерно в 2 раза больше числа Маха конвекции, что позволяет использовать это и последующие соотношения до чисел Маха собственно струи равного двум. Эту зависимость иногда называют «законом четвертой степени» от скорости, что легко видеть.