Структура и режимы течения в неизобарических сверхзвуковых струях, страница 13

Поясним физику образования квадрупольного шума в турбулентном потоке. Оценка величины членов в тензоре T_ij показывает, что член вязких напряжений p_ij пропорционален величине  и при обычных условиях истечения струй является значительно меньше первого члена, описывающего напряжения Рейнольдса. Фактически тензор - это количество движения единичного объема ru_i переносимое в направлении x_i переносимое со скоростью u_j в направлении x_j. Так как перенос симметричен во все стороны, то элемент жидкости, находящий под действием импульса ru_i испытывает с двух сторон воздействие равных по величине, но противоположно направленных сил. Как было отмечено ранее, воздействие силы на элемент среды эквивалентно эффекту дипольного источника. Пара равных по величине и противоположных по направлению сил эквивалентна двум противоположно ориентированным диполям, т.е. квадруполю. Интенсивность квадруполей характеризуется тензором плотности количества движения T_ij. Схема генерации квадруполей и направленность излучения звука приведена на рис. 50. Если квадруполь продольный и диполи образующие его параллельны друг другу и пульсируют в противофазе, то диаграмма направленности пропорциональна квадрату косинуса, так как направленность диполя пропорциональна косинусу угла. Если квадруполь поперечный, то излучение одного из диполей сдвинуто на 90° и диаграмма направленности представляет собой произведение косинуса на синус. В свою очередь квадруполь можно представить в виде системы из четырех диполей пульсирующих парами в противофазе (продольный квадруполь) или каждый относительно другого со сдвигом по фазе на 90° (обычный квадруполь).

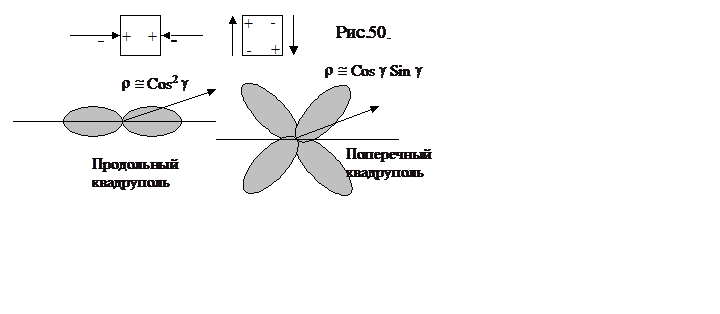Используя порядковые оценки для производных по времени и порядковую оценку для тензора T_ij из соотношения (15.4,а) получаем после подстановки оценок в (15.14) для пульсаций плотности

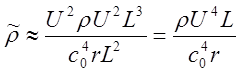                                           .                                     (15.15)

Подставляя (15.15) в (15.6) получаем для звуковой мощности квадрупольного источника выражение

                                                                               (15.16)

Из (15.16) видно, что с ростом числа Маха мощность излучения квадрупольных источников опережает все остальные. Это известный «закон восьмой степени» от скорости, справедливый для чисел Маха струй вплоть до двух.

Примером шума преимущественно квадрупольного характера является шум реактивных и высокоскоростных воздушных струй.

15.1.5. Влияние конвекции на направленность излучения шума.

Так как монопольное излучение изотропно, а ориентация диполей и квадруполей случайна, то шум струи должен быть также практически изотропным. Небольшая изотропия возможна только из-за наличия длины струи. Тем не менее, из-за движения потока в излучении звука появляется выделенное направление и влияние его на направленность звука становится тем больше, чем больше скорость. Так как при больших скоростях, но меньших скорости звука в слое смешения, излучают преимущественно квадрупольные источники турбулентного потока, то имеет смысл рассмотреть только этот случай. Решением уравнения (15.4) без упрощений будет соотношение

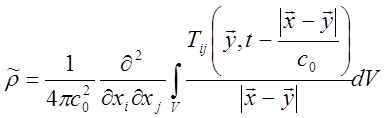                                                             (15.17)

Из-за движения источника звука он непрерывно меняет свое местоположение и эффективный объем вихря вытягивается в направлении движения. Введем новую координату x, которую он имел на момент излучения звука.

                                                                                                   (15.18)

Здесь М_к – число Маха скорости конвекции источника звука в потоке. Тогда соотношение для дифференциалов объемов источника будет

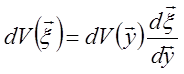
или учитывая (15.18)

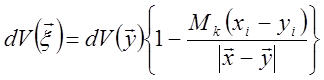
Тогда уравнение (15.17) запишется в таком виде

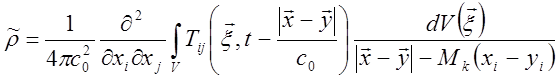                                           (15.19)