![]()
Последний член является константой и в рассмотрении не принимает участия. Первый член связан с собственным турбулентным шумом струи был ранее рассмотрен в п. 15.1.4, второй член связан со сдвиговым шумом. Переходя к трехмерному случаю движений газа уравнение (15.4) можно записать как
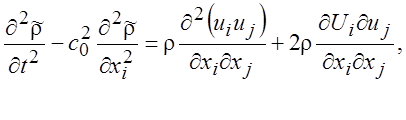 (15.22)
(15.22)
По аналогии с выкладками п. 15.1.4, члены справа в уравнении (15.22) являются источниковыми членами. Решение уравнения (15.22) будет иметь вид аналогичный предыдущим. После внесения производных от координаты х под интеграл и дифференцирования интеграл можно записать в виде суммы интегралов, в которые входит член с чисто пульсационной составляющей собственного шума турбулентной струи и член с составляющими, включающими среднюю скорость U, сдвигового шума
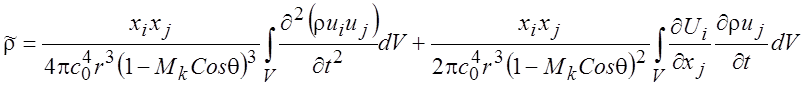 (15.23)
(15.23)
Знаменатель
с числом Маха конвекции вихрей во втором члене имеет меньший показатель из-за
однократного преобразования ко временной производной, так как первый
сомножитель не зависит от времени. Интеграл во втором члене (15.23) содержит
производную по координате от средней скорости, ответственную за сдвиг в потоке.
Сопоставляя второй сомножитель со вторым сомножителем интеграле с (15.2)
получаем, что сдвиговый шум имеет дипольный характер, типа порождаемого
переменной силой Fi. И зависимость
его интенсивности от угла q
также характерна для дипольного излучения звука (см. рис. 48). Однако, в
отличие от хаотического дипольного шума турбулентных пульсаций, излучение имеет
выделенное направление и ориентировано поперек градиента средней скорости, т.е.
вдоль оси струи. Таким образом, учитывая связь между интенсивностью I и пульсациями плотности ![]() (15.21),
получаем, что интенсивность собственного шума I
зависит от угла q как фактор
(15.21),
получаем, что интенсивность собственного шума I
зависит от угла q как фактор 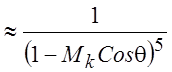 (с учетом сокращения числа источников), а
сдвигового шума как фактор
(с учетом сокращения числа источников), а
сдвигового шума как фактор 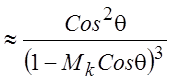 (с учетом сокращения
числа источников). Направленность сдвигового шума и влияние конвекции и
рефракции звука проиллюстрированы на рис. 52.
(с учетом сокращения
числа источников). Направленность сдвигового шума и влияние конвекции и
рефракции звука проиллюстрированы на рис. 52.
При малых числах Маха
конвекции Мк знаменатель в факторах изменяется мало и направленность
сдвигового шума определяет квадрат косинуса. Это приводит к так называемому
обратному эффекту Допплера, когда частота шума струи уменьшается при уменьшении
угла между направлением течения струи и направлением измерения. Для всех
движущихся источников частота звука определяется угловым фактором 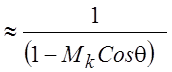 . Этот же фактор в равной степени управляет
частотой как собственного, так и сдвигового шума струи. Но частота собственного
шума вдвое выше частоты сдвигового шума струи, так как в турбулентном потоке
. Этот же фактор в равной степени управляет
частотой как собственного, так и сдвигового шума струи. Но частота собственного
шума вдвое выше частоты сдвигового шума струи, так как в турбулентном потоке ![]() и для собственного шума
и для собственного шума ![]() , а для сдвигового шума
, а для сдвигового шума ![]() . Так как направленность сдвигового шума
для малых Мк более острая вдоль оси струи, то при уменьшении угла q превалирует низкочастотный сдвиговый
шум, а не более высокочастотный, как это следовало бы из эффекта Допплера. Этот
эффект наиболее заметен на слух, когда перед наблюдателем по полю аэродрома
маневрирует реактивный пассажирский лайнер, турбины работают на низких оборотах
и скорость струи небольшая. Когда лайнер стоит боком к наблюдателю шум
невыносимо высокочастотный, а по мере разворота самолета соплами двигателей к наблюдателю
ощущается терпимый низкочастотный рев.
. Так как направленность сдвигового шума
для малых Мк более острая вдоль оси струи, то при уменьшении угла q превалирует низкочастотный сдвиговый
шум, а не более высокочастотный, как это следовало бы из эффекта Допплера. Этот
эффект наиболее заметен на слух, когда перед наблюдателем по полю аэродрома
маневрирует реактивный пассажирский лайнер, турбины работают на низких оборотах
и скорость струи небольшая. Когда лайнер стоит боком к наблюдателю шум
невыносимо высокочастотный, а по мере разворота самолета соплами двигателей к наблюдателю
ощущается терпимый низкочастотный рев.
15.2. Особенности шума сверхзвуковых струй.
15. 2.1. Волны Маха
В сверхзвуковых струях,
когда число Маха струи превышает двойку, наряду с турбулентным шумом появляется
дополнительный источник шума, так называемый шум волн Маха. Он
возникает, когда скорость газа в слое смешения струи превышает скорость звука
во внешней среде. Тогда вихри, формирующиеся в слое смешения, движутся по
отношению к внешнему потоку со сверхзвуковой скоростью и каждый элементарный
вихрь создает слабую ударную волну во внешней среде (см. рис. 52). Угол наклона
фронта такой  волны составляет
волны составляет 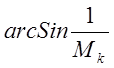 ,
поэтому угол между направлением распространения волн к оси струи будет
определяться как
,
поэтому угол между направлением распространения волн к оси струи будет
определяться как 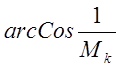 . Этот тип шума имеет наибольшую
интенсивность на начальном участке сверхзвуковой струи, вблизи сопла, когда
слой смешения струи очень тонкий. На теневых фотографиях он выглядит как пучок
волн исходящий из области первой бочки струи под углом к оси струи (см. рис.
53). Для практических расчетов угол распространения волн Маха можно оценивать
по соотношению
. Этот тип шума имеет наибольшую
интенсивность на начальном участке сверхзвуковой струи, вблизи сопла, когда
слой смешения струи очень тонкий. На теневых фотографиях он выглядит как пучок
волн исходящий из области первой бочки струи под углом к оси струи (см. рис.
53). Для практических расчетов угол распространения волн Маха можно оценивать
по соотношению
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.