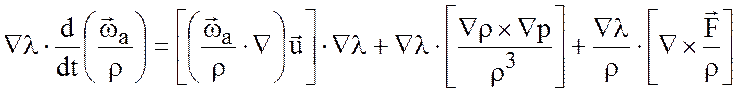 . (3.25)
. (3.25)
Сложив (3.23) и (3.25) и учитывая при этом (3.22), получаем следующее выражение
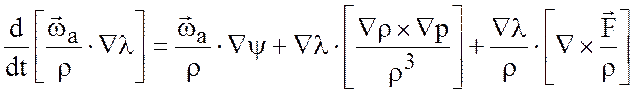 . (3.26)
. (3.26)
Уравнение (3.26) является основным соотношением теоремы Эртеля.
Теорема (Эртель). Если отсутствуют вязкие силы ![]() , источников не существует
, источников не существует ![]() и жидкость баротропна, т.е.
и жидкость баротропна, т.е. ![]() или
или ![]() , тогда
потенциальный вихрь Эртеля
, тогда
потенциальный вихрь Эртеля
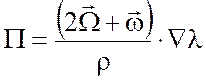
сохраняется вдоль траектории при движении жидкости, то есть
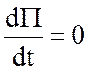 .
.
Действительно, в силу условия
баротропности жидкости ![]() , так как
, так как 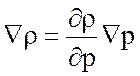 . Условие
. Условие ![]() можно
обобщить как
можно
обобщить как ![]() .Тогда, если
.Тогда, если ![]() , то
, то
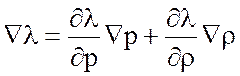
Откуда следует, что ![]() . Таким образом из (3.26) в условиях
теоремы сразу получаем
. Таким образом из (3.26) в условиях
теоремы сразу получаем
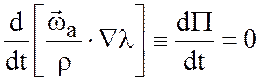 .
.
Потенциальный вихрь имеет важное значение
для качественного анализа движений планетарного масштаба. Некоторым парадоксом
в факте введения этой характеристики является то, что потенциальный вихрь даже
не имеет размерности вихря. Однако, этот термин является уже установившимся и
его широкое использование позволяет получить многие качественные результаты по
принципам движения жидкости в геофизической гидродинамике. Вообще говоря,
теорема Эртеля представляет собой теорему Кельвина при специально выбранном
контуре ![]() , лежащем на поверхностях постоянных
значений
, лежащем на поверхностях постоянных
значений ![]() . Пояснения здесь могут быть следующими.
Если потенциальный вихрь
. Пояснения здесь могут быть следующими.
Если потенциальный вихрь ![]() сохраняется, когда
расстояние между двумя изоповерхностями
сохраняется, когда
расстояние между двумя изоповерхностями ![]() увеличивается,
то градиент
увеличивается,
то градиент ![]() будет уменьшаться. Тогда компонента
будет уменьшаться. Тогда компонента ![]() должна увеличиваться для сохранения
должна увеличиваться для сохранения ![]() . Если изменения
. Если изменения ![]() невелики,
то должен увеличиваться абсолютный вихрь
невелики,
то должен увеличиваться абсолютный вихрь ![]() . Таким
образом, удаления изоповерхностей
. Таким
образом, удаления изоповерхностей ![]() , например, плотности
будет создавать относительную завихренность за счет изменения абсолютной
завихренности.
, например, плотности
будет создавать относительную завихренность за счет изменения абсолютной
завихренности.
С другой стороны, ![]() и
и
![]() , являясь инвариантами, создают на
пересечении изолиний трубки лагранжевых инвариантов, по которым движется
жидкость.
, являясь инвариантами, создают на
пересечении изолиний трубки лагранжевых инвариантов, по которым движется
жидкость.
4. Основные упрощающие приближения.
4.1. Приближение Буссинеска.
Система уравнений (2.16) представляет собой полную модель, описывающую гидротермодинамику жидкости во вращающейся системе координат, в нее включены практически все процессы динамики атмосферы и океана, включая акустические волны и влияние сферичности Земли. Однако, для анализа некоторых явлений нам достаточно использовать более простые постановки, которые позволят сосредоточить внимание на характерных особенностях процессов, не затеняя их смысл несущественными деталями. В каждом случае мы будем указывать пределы применимости упрощающих приближений и усложнять модели, по мере необходимости, при описании процессов различного масштаба и сложности.
Выпишем исходную систему уравнений (2.16), опуская диффузионные и вязкие члены, считая жидкость несжимаемой
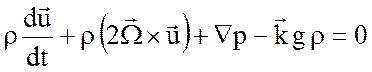 , (4.1)
, (4.1)
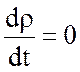 , (4.2)
, (4.2)
![]() . (4.3)
. (4.3)
Здесь ![]() -
единичный вектор, направленный по оси
-
единичный вектор, направленный по оси ![]() , где
, где ![]() ,
, ![]() -
радиус Земли,
-
радиус Земли, ![]() - ускорение свободного падения.
- ускорение свободного падения.
Можно выделить состояние
статического равновесия ![]() . Из (4.1) следует, что
. Из (4.1) следует, что
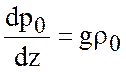 . Будем искать решения, близкие к состоянию
статического равновесия. Возьмем
. Будем искать решения, близкие к состоянию
статического равновесия. Возьмем ![]() ,
, ![]()
![]() . Считая изменения
. Считая изменения ![]() и
и ![]() малыми,
из (4.2) следует, что
малыми,
из (4.2) следует, что
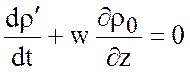 ,
,
а из (4.1)
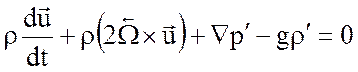 .
.
Если записать 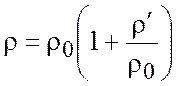 , где
, где
·
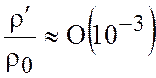 для океана,
для океана,
· 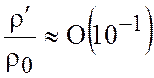 для атмосферы,
для атмосферы,
то положив 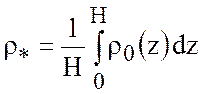 , линеаризуем (4.4)
, линеаризуем (4.4)
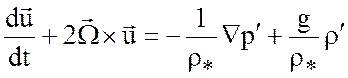 .
.
В итоге, опустив штрихи, получим приближение Буссинеска
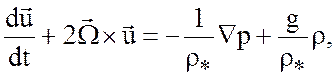
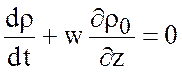 (4.4)
(4.4)
![]()
4.2. Приближение ![]() - плоскости.
- плоскости.
В ряде случаев, когда
характерный масштаб движений меньше радиуса Земли, удобно использовать систему
координат с начальной точкой, выбранной на поверхности Земли, на некоторой
широте ![]() . Являясь, вообще говоря, криволинейной, эта
система уравнений при определенных условиях приводится к виду, аналогичному
прямоугольной декартовой системе, что облегчает многие рассмотрения. Проведем
указанные преобразования. Для сферической системы координат
. Являясь, вообще говоря, криволинейной, эта
система уравнений при определенных условиях приводится к виду, аналогичному
прямоугольной декартовой системе, что облегчает многие рассмотрения. Проведем
указанные преобразования. Для сферической системы координат ![]() в приближении Буссинеска система (4.1) -
(4.3) примет вид
в приближении Буссинеска система (4.1) -
(4.3) примет вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.