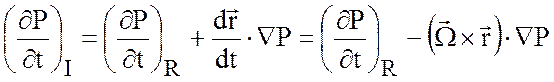 ,
,
а
![]() ,
,
откуда
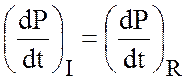 .
.
Таким образом, уравнение сохранения массы (2.2) и все термодинамические соотношения от (2.3) до (2.9) не зависят от выбора системы отсчета и, следовательно, могут применяться непосредственно для описания движения во вращающейся системе координат.
Поскольку градиенты величин инвариантны во вращающейся и инерциальной системах , а ньютоновское трение не меняется при переходе от одной системе к другой, то окончательно, система уравнений движения и притока тепла во вращающейся системе координат будет иметь вид
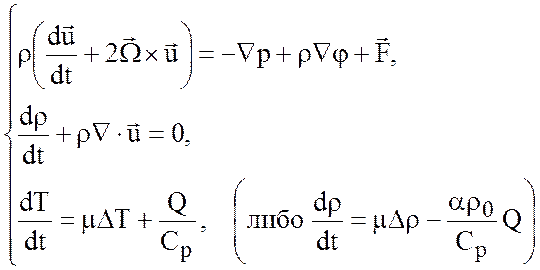 (2.16)
(2.16)
где ![]() -
скорость, наблюдаемая во вращающейся системе отсчета, а первый закон
термодинамики записан для чистой воды.
-
скорость, наблюдаемая во вращающейся системе отсчета, а первый закон
термодинамики записан для чистой воды.
3. Основные понятия.
3.1. Относительный и планетарный вихрь.
Механизмы, которые управляют процессами геофизической гидродинамики, настолько сложны, что нахождение решения полной системы нелинейных уравнений требует использования всего мощного инструмента численного моделирования для их реализации. Однако применение приближенных методов требует понимания основных принципов и механизмов, управляющих процессами во вращающихся жидкостях планетарного масштаба. Можно получить несколько общих принципов, являющихся полезными как в случае классической гидродинамики, так и в случае анализа геофизических явлений. Эти положения базируются на динамических механизмах, которые могут быть скрыты при решении отдельной проблемы. Все эти положения и теоремы могут быть исследованы на качественном уровне с достаточно содержательным наполнением.
В ряду динамических
характеристик в геофизической гидродинамике особо важную роль играет вектор
вихря ![]() , являющийся ротором поля скорости
, являющийся ротором поля скорости ![]() . В декартовой системе координат
. В декартовой системе координат ![]() с компонентами скорости
с компонентами скорости ![]() имеет место формула
имеет место формула
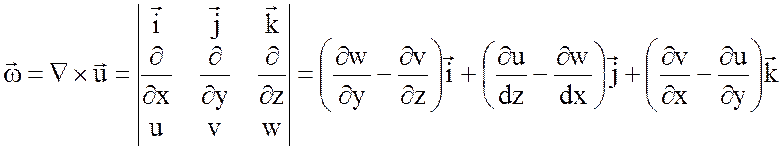 .
.
Если, например, вектор скорости ![]() , то вихрь направлен вдоль оси
, то вихрь направлен вдоль оси ![]() и равен по модулю
и равен по модулю ![]() .
Отсюда видно, что для того, чтобы движение жидкости имело ненулевую
завихренность, не обязательно наличие искривленных траекторий, достаточно,
чтобы течение имело сдвиг.
.
Отсюда видно, что для того, чтобы движение жидкости имело ненулевую
завихренность, не обязательно наличие искривленных траекторий, достаточно,
чтобы течение имело сдвиг.
При вращении жидкости как
твердого тела с угловой скоростью ![]() , т.е. когда
, т.е. когда ![]() , имеем
, имеем ![]() .
Действительно, для любых векторов
.
Действительно, для любых векторов ![]() и
и ![]() справедлива формула
справедлива формула
![]() , (3.1)
, (3.1)
при ![]() получим
получим
![]() ,
,
здесь учитывалось
1. ![]() ,
,
2. 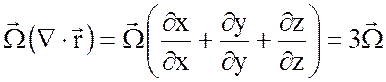 ,
,
3. 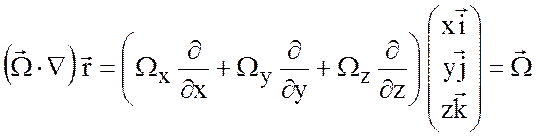 .
.
Более наглядным образом этот результат можно получить на основе теоремы Стокса
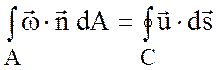 (3.2)
(3.2)
Здесь интеграл берется по поверхности ![]() , охваченной контуром
, охваченной контуром ![]() ,
, ![]() -
нормаль к поверхности
-
нормаль к поверхности ![]() ,
, ![]() -
касательный вектор к контуру
-
касательный вектор к контуру ![]() .
.
Используя теорему о среднем, из (3.2) для
малого элемента ![]() имеем
имеем
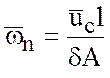 ,
,
где ![]() -
средняя величина
-
средняя величина ![]() по площади
по площади ![]() ,
, ![]() - длина
контура
- длина
контура ![]() ,
, ![]() -
средняя касательная скорость. Если
-
средняя касательная скорость. Если ![]() - малый круг радиуса
- малый круг радиуса ![]() , то
, то
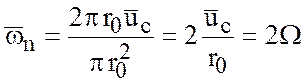 .
.
Вихрь, наблюдаемый в инерциальной
системе отсчета, называется абсолютным вихрем и определяется как ![]() , здесь
, здесь ![]() -
относительный вихрь и
-
относительный вихрь и ![]() - планетарный вихрь. Компонента
планетарного вихря, перпендикулярная к поверхности Земли, равна параметру
Кориолиса
- планетарный вихрь. Компонента
планетарного вихря, перпендикулярная к поверхности Земли, равна параметру
Кориолиса ![]() , где
, где ![]() -
широта точки
-
широта точки 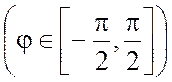 . Если описывать вертикальную
компоненту относительного вихря, то
. Если описывать вертикальную
компоненту относительного вихря, то 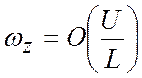 , где
, где ![]() - горизонтальная скорость,
- горизонтальная скорость, ![]() - характерный горизонтальный масштаб.
Отношение
- характерный горизонтальный масштаб.
Отношение
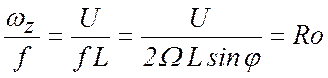
определяет безразмерный параметр - локальное число Россби.
Вне экваториальной зоны ![]() , и для течений с малым числом Россби относительный
вихрь мал по сравнению с планетарным. Таким образом, крупномасштабные течения
никогда не являются безвихревыми. Их завихренность в основном создается
планетарным вихрем. Так как вихрь
, и для течений с малым числом Россби относительный
вихрь мал по сравнению с планетарным. Таким образом, крупномасштабные течения
никогда не являются безвихревыми. Их завихренность в основном создается
планетарным вихрем. Так как вихрь ![]() определяется как
определяется как ![]() , то очевидно,
, то очевидно,
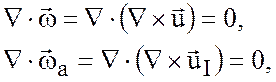
Следовательно вихрь бездивергентен, то
есть линии постоянного вихря не пересекаются. Таким образом, можно ввести
понятия вихревой нити и вихревой трубки. Вихревая нить - линия, касательные к
которой в каждой точке совпадают с направлением ![]() .
Вихревые нити планетарного вихря - прямые, параллельные оси вращения. Вихревая
трубка - набор вихревых нитей, ограниченных некоторой поверхностью, проходящих
через замкнутый контур.
.
Вихревые нити планетарного вихря - прямые, параллельные оси вращения. Вихревая
трубка - набор вихревых нитей, ограниченных некоторой поверхностью, проходящих
через замкнутый контур.
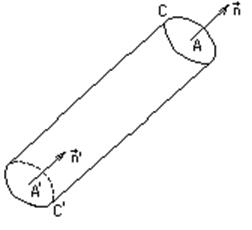
Рис. 3.1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.