Предмет геофизической гидродинамики. Уравнения движения. Основные упрощающие приближения, страница 7

При наличии вязкости вихревые нити уже не обязаны состоять из одних и тех же частиц, а бароклинные эффекты могут создавать новые вихревые нити.

3.4. Уравнение вихря.

Циркуляция характеризует скалярную меру завихренности. Вихрь является вектором, поэтому законы изменения циркуляции дают неполную картину векторной динамики поля вихря. Для исследования природы вихря выведем уравнение для вектора относительного вихря.

Преобразуем уравнение движения:

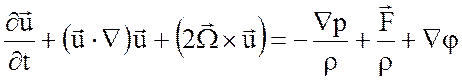.                             (3.4)

В формуле

положим , тогда

.

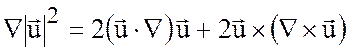Так как вектор вихря определяется как ротор поля скорости , то

.

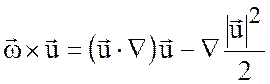Подставим отсюда значение  в (3.4) и получим форму Громеки-Лэмба

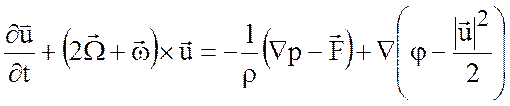.                      (3.5)

Применим операцию ротора к (3.5)

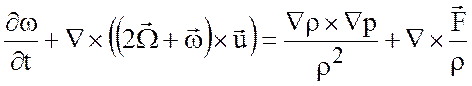.                                          (3.6)

По формуле двойного векторного произведения (3.1)

,

здесь слагаемое , так как . Тогда, (3.6) примет вид

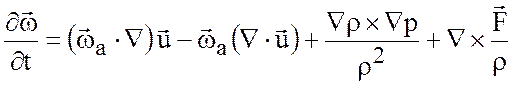,                      (3.7)

где, по определению  - абсолютный вихрь жидкой частицы, наблюдаемый в инерциальной, невращающейся системе отсчета;  - планетарный вихрь;  - относительный вихрь, то есть вихрь относительной скорости.

Скорость изменения абсолютного вихря движущейся жидкой частицы определяется четырьмя членами в правой части уравнения (3.7). Последние два члена в правой части представляют собой бароклинный вектор и ротор силы трения. Обсуждение этих источников вихря уже была дана при обсуждении скорости изменения циркуляции. Первые два члена в правой части рассмотрим особо.

Рассмотрим произвольную точку  в жидкости и выберем локальную декартову систему координат так, чтобы в точке  ось  была касательной к нити абсолютного вихря, проходящего через точку . В этой системе координат в точке , где  - единичный вектор вдоль оси . Далее, в точке  первые два члена в правой части (3.7) могут быть записаны так

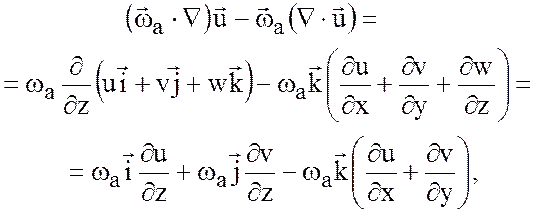                   (3.8)

где ,  и  представляют собой единичные векторы вдоль осей ,  и , соответственно. Компоненты относительной скорости по осям ,  и  обозначаем через ,  и .

Рассмотрим теперь скорость изменения компоненты вихря параллельной оси . В соответствии с  (3.8) изменение -компоненты вихря в отсутствие бароклинности и трения дается формулой

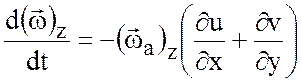,                                      (3.9)

т.е. равно отрицательному произведению исходного абсолютного вихря на дивергенцию вектора скорости в плоскости, перпендикулярной . Если дивергенция отрицательна 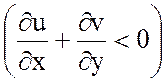, то нити абсолютного вихря будут собираться, становясь ближе друг к другу и увеличивая величину вектора вихря, одновременно уменьшая площадь поперечного сечения локальной вихревой трубки в соответствии с теоремой Кельвина. Действительно, можно показать, что

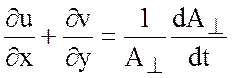                                                 (3.10)

где  - элементарная площадка в плоскости , . Таким образом, (3.9) может быть записано как

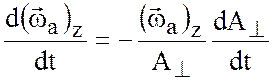                                           (3.11)

или

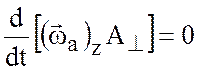,                                                     (3.12)

что, очевидно, эквивалентно теореме Кельвина. Описанный механизм увеличения компоненты вихря в направлении нити известен как механизм растяжения вихревой трубки, так как уменьшение площади поперечного сечения трубки в несжимаемой жидкости может быть достигнуто только за счет вытягивания жидкой трубки вдоль её длины так, чтобы объем её сохранился.

 Из формулы (3.8) следует, что существует еще один механизм изменения вихря. Рассмотрим скорость увеличения компоненты вихря в направлении, перпендикулярном вихревой нити, например, в направлении оси . В соответствии с (3.8) скорость увеличения этой компоненты равна 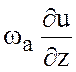, и по прошествии времени

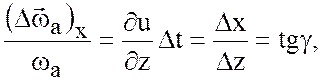
отсюда

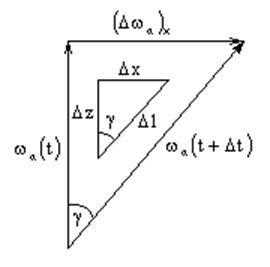
где  - проекция на ось  элемента жидкой линии , который первоначально был параллелен  и имел длину . Из-за сдвига поля скорости этот элемент жидкой линии наклоняется на угол , и из рисунка видно, что возникает параллельная оси  компонента вихря, равная -компоненте вектора вихря в момент времени , который сам наклоняется на тот же угол, что и жидкая линия. Это есть не что иное, как проявление того факта, что нити абсолютного вихря в отсутствие других эффектов движутся вместе с жидкостью. Аналогичные соображения применимы и к -направлению.