Таким образом, скорость изменения относительного вихря обусловлена следующими факторами:
1. генерацией вихря бароклинностью;
2. диффузией из-за процессов трения;
3. растяжением трубок абсолютного вихря, которое изменяет компоненту вихря, параллельную нити, из-за конвергенции вихревых нитей;
4. наклоном вектора вихря, вызываемым изменением вдоль вихревой нити компоненты скорости, перпендикулярной этой нити.
Важно отметить, что если ![]() первоначально равнялся нулю, то изгиб и
конвергенция нитей абсолютного вихря из-за относительного движения жидкости в
поле планетарного вихря будут в отсутствие других эффектов создавать
относительный вихрь.
первоначально равнялся нулю, то изгиб и
конвергенция нитей абсолютного вихря из-за относительного движения жидкости в
поле планетарного вихря будут в отсутствие других эффектов создавать
относительный вихрь.
3.4. Термический ветер. Теорема Тейлора-Праудмена.
Из соотношения уравнения вихря можно извлечь некоторые ограничения на движение жидкости.
При ![]() движение
имеет планетарный масштаб. Предположив, что
движение
имеет планетарный масштаб. Предположив, что ![]() и
и ![]() , в уравнении вихря (3.7) можно отбросить
часть, связанную с относительным вихрем
, в уравнении вихря (3.7) можно отбросить
часть, связанную с относительным вихрем
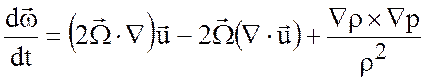 . (3.13)
. (3.13)
Оценим роль ![]() в
уравнении для вихря, если число Россби мало:
в
уравнении для вихря, если число Россби мало:
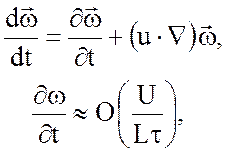
где ![]() -
характерное время. Тогда характерный масштаб
-
характерное время. Тогда характерный масштаб ![]() ,
отнесенный к масштабу
,
отнесенный к масштабу ![]() , имеет вид
, имеет вид
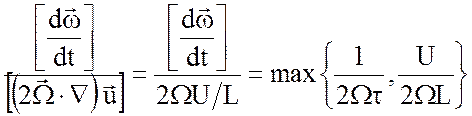 .
.
Мы изучаем явления, для
которых характерное время порядка 10 суток, а характерный размер достаточно большой.
Отсюда ![]() и
и ![]() -
малы. Для Гольфстрима, например,
-
малы. Для Гольфстрима, например, ![]() см/с,
см/с, ![]() км, следовательно,
км, следовательно, ![]() .
Таким образом, в соотношении (3.13) можно пренебречь членом
.
Таким образом, в соотношении (3.13) можно пренебречь членом ![]() , что дает следующее соотношение
, что дает следующее соотношение
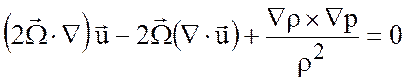 . (3.14)
. (3.14)
Для простоты считаем систему
координат такой, что ось ![]() параллельна вектору вращения
параллельна вектору вращения
![]() , тогда соотношение (3.14) примет вид
, тогда соотношение (3.14) примет вид
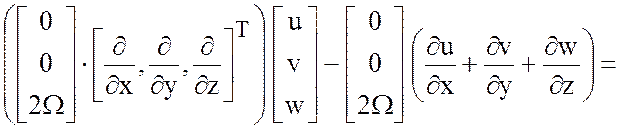
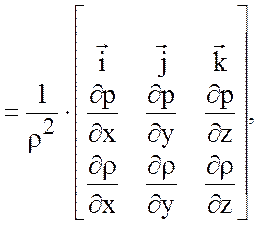 (3.15)
(3.15)
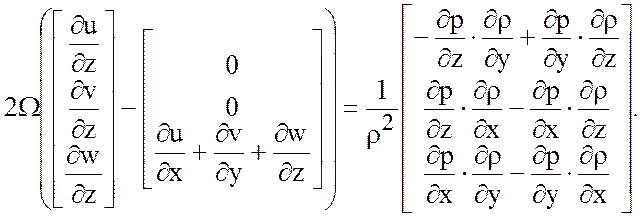
Откуда следуют уравнения термического ветра:
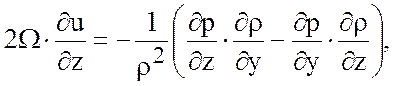
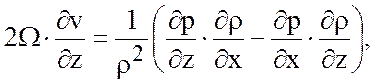 (3.16)
(3.16)
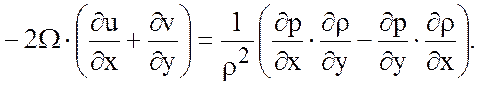
можно показать, что члены в правой части третьего уравнения
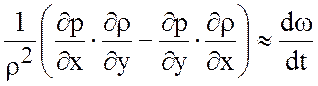
и ими можно пренебречь. Тогда из третьего уравнения системы (3.16) следует, что движение термического ветра бездивергентно
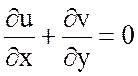 . (3.17)
. (3.17)
Если жидкость несжимаема, то 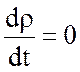 . Из закона сохранения массы
. Из закона сохранения массы 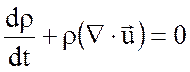 следует, что
следует, что ![]() .
Учитывая (3.17), получаем
.
Учитывая (3.17), получаем 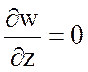 . Таким образом, с
точностью до числа Россби, движение атмосферы квазигоризонтально по
направлениям, перпендикулярным вектору вращения. Если на некотором уровне
вертикальная скорость равна нулю, то она равна нулю во всем столбе жидкости.
Этот результат известен как теоремой Тейлора-Праудмена.
. Таким образом, с
точностью до числа Россби, движение атмосферы квазигоризонтально по
направлениям, перпендикулярным вектору вращения. Если на некотором уровне
вертикальная скорость равна нулю, то она равна нулю во всем столбе жидкости.
Этот результат известен как теоремой Тейлора-Праудмена.
3.5. Потенциальный вихрь и теорема Эртеля.
Теорема Кельвина дает сильный результат, но она представляет собой интегральную теорему, имеющую дело со скаляром и требующую знания эволюции жидких поверхностей. Кроме того, она справедлива лишь в отсутствие бароклинных эффектов. Уравнение вихря имеет важное значение, в геофизической гидродинамике поскольку оно описывает изменение относительного и абсолютного вихря с учетом их векторного характера, однако оно дает лишь описание того, как изменяется вихрь. Весьма полезный закон сохранения, свободное от упомянутых недостатков, было получено Эртелем в 1942 г.
Вектор вращения ![]() -
постоянный вектор, поэтому уравнение (3.7) может быть записано как
-
постоянный вектор, поэтому уравнение (3.7) может быть записано как
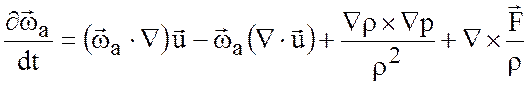 . (3.18)
. (3.18)
Уравнение неразрывности дает
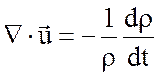 , (3.19)
, (3.19)
и по правилу дифференцирования частного имеем
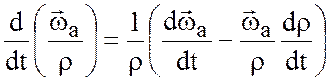 , (3.20)
, (3.20)
Умножаем (3.18) на ![]() и
воспользуемся (3.19) и (3.20). Тогда (3.18) переписывается в виде
и
воспользуемся (3.19) и (3.20). Тогда (3.18) переписывается в виде
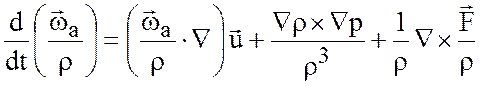 . (3.21)
. (3.21)
Рассмотрим теперь некоторую скалярную
характеристику жидкой частицы ![]() , удовлетворяющую
уравнению вида
, удовлетворяющую
уравнению вида
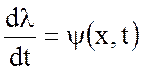 , (3.22)
, (3.22)
где ![]() -
некоторый источник
-
некоторый источник ![]() . Например,
. Например, ![]() может быть:
может быть:
1. ![]() -
потенциальная температура;
-
потенциальная температура;
2. ![]() -
плотность;
-
плотность;
3. ![]() -
соленость.
-
соленость.
Имеет место следующая формула
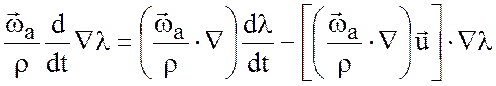 . (3.23)
. (3.23)
Действительно,
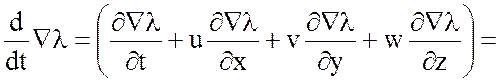
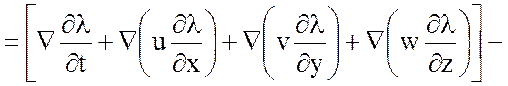 (3.24)
(3.24)
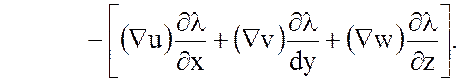
Теперь, умножая скалярно (3.24) на ![]() , получаем требуемое равенство (3.23).
Умножив (3.21) скалярно на
, получаем требуемое равенство (3.23).
Умножив (3.21) скалярно на ![]() , имеем
, имеем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.