Предмет геофизической гидродинамики. Уравнения движения. Основные упрощающие приближения, страница 2

1. Введение. Предмет геофизической гидродинамики.

Выделение геофизической гидродинамики как направления гидродинамики произошло в начале 70-х годов. Оно было оформлено созданием  Джозефом Смагоринским в Принстонском университете Лаборатории геофизической гидродинамики. Что же рассматривает геофизическая гидродинамика? Она занимается изучением процессов, происходящих в жидких и газообразных средах планет и звезд, и имеет приложения в метеорологии, океанологии, климатологии, физике мантии Земли, планетологии и астрофизике. Геофизическую гидродинамику можно определить как гидродинамику природных течений вращающихся, бароклинных, стратифицированных жидкостей и газов. Рассмотрим более подробно эти факторы.

1. Вращение. Все планеты вращаются вокруг своей оси. Земля имеет радиус  и угловую скорость вращения . В системе отсчета, связанной с вращающейся Землей, вращение создает, во-первых, центробежную силу, не оказывающую существенного влияния на движение атмосферы и океана, и, во-вторых, более важную, действующую на движение с относительной скоростью силу Кориолиса , отклоняющую частицы в северном полушарии вправо от направления движения. Это создает понятие так называемой "геострофичности", когда в отличие от обычной  гидродинамики движение происходит не от зон большего давления к меньшему, а вдоль изолиний давления. Так, в зоне повышенного давления  "антициклон" движение происходит по часовой стрелке. Но это характерно не для всех движений в атмосфере или океане. Для этого движения должны быть достаточно большими. Что это значит? Пусть характерный масштаб скорости движения  в атмосфере равен 20 м/с. Тогда для того, чтобы вращение Земли влияло на движение, отношение характерного пространственного масштаба движений  к скорости движений  должно быть больше или равно периоду вращения Земли, равного суткам, то есть .Отсюда, характерный масштаб движений должен быть порядка тысячи километров  км. При этом безразмерная величина 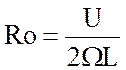 - число Россби, будет  малой величиной . Для океана характерная скорость в Гольфстриме  м/с, при ширине течения  км дает значение параметра Россби . Эта величина является характеристикой "планетарности" движений, то есть зависимости движений от планетарных движений и, в частности, от вращения.

2. Стратифицированность. Прежде всего, необходимо отметить, что выбранные таким образом крупномасштабные движения являются движениями в узкой пленке жидкости. В самом деле, если горизонтальный масштаб движений  м (1000 км), и для океана  м (4 км), для атмосферы  м (50 км), то отношение  вертикального масштаба движений к горизонтальному будет   для океана и  для атмосферы. Однако это не означает, что движение в атмосфере и океане является полностью двумерными в этой пленке, так как разность температур на поверхности и в глубине океана может достигать , а в атмосфере . При этом типичное распределение плотности в океане имеет максимальный вертикальный градиент в верхнем слое 1.5 км, который называется термоклин, и поэтому стратификация (расслоенность) по плотности в океане и в атмосфере весьма велика. Типичное распределение температуры с глубиной в океане имеет вид:

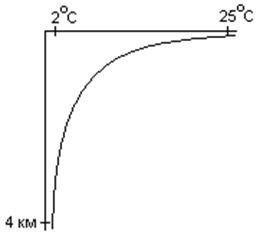
                                                       Рис1.1.

Параметр, характеризующий стратификацию,  может быть записан в виде отношений двух масштабов  - радиуса деформации Россби к  - характерному масштабу движений. В результате получаем число Бургера . Радиус деформации Россби дается выражением, зависящим от уровня стратификации  на глубине 

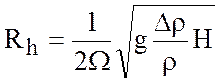
Здесь - ускорение свободного падения.

3. Бароклинность. Бароклинность означает, что в объеме жидкости поверхности постоянного давления (изобарические поверхности) и  поверхности постоянной плотности (изопикнические поверхности) не совпадают. В океане это, например, означает, что уравнение состояния для плотности имеет вид , где  - температура,  - соленость,  - давление. Это, в частности, является следствием стратификации и вызывает движения. Если бы  плотность жидкости зависела только от давления, то изобарические и изопикнические поверхности совпадали и движения происходили бы во всей толще жидкости как единое целое под действием градиентов давления.