Предмет геофизической гидродинамики. Уравнения движения. Основные упрощающие приближения, страница 6

Так как вихрь бездивергентен, то для любого объема  (объема вихревой трубки, ограниченной двумя поверхностями )

,

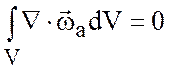а значит,

,

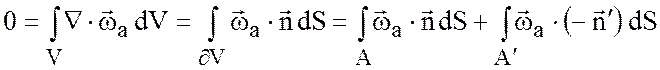где  - нормаль к поверхности ,  - нормаль к поверхности .

Определим интенсивность вихревой трубки  по формуле

.

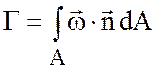Заметим, что

.

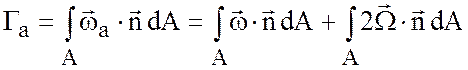То есть интенсивность вихревой трубки постоянна вдоль ее длины

,

где  - площадь проекции  на плоскость, перпендикулярную .

3.2. Циркуляция. Уравнение изменения циркуляции.

Существует еще один способ измерения интенсивности вихревой трубки. По теореме Стокса поток абсолютного вихря через поверхность , ограниченную замкнутым контуром  равен

,

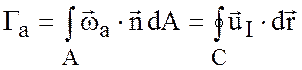где . Величина 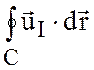 называется циркуляцией абсолютной скорости . Циркуляции относительной скорости  дается выражением

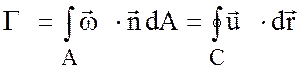
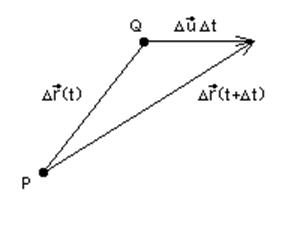
Рис. 3.2.

Рассмотрим скорость изменения относительной циркуляции в случае, когда  - контур, состоящий из одних и тех же частиц и движущийся вместе с жидкостью.

.

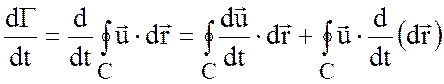Заметим, что

,

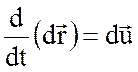поскольку  (см. рис. 3.2), значит,

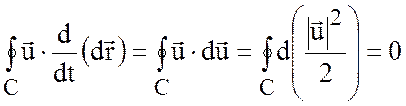
как интеграл от полного дифференциала по замкнутому контуру. Таким образом, скорость изменения относительной циркуляции равна контурному интегралу по  от относительного ускорения. Из уравнений движения следует

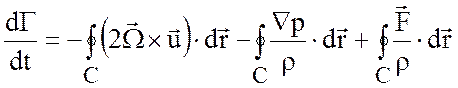                               (3.3)

Здесь учтено, что контурный интеграл от  обращается в ноль на замкнутом контуре. В соответствии с (3.3) существует три механизма, которые отвечают за изменение циркуляции :

1. Циркуляция силы Кориолиса, отнесенная к единице массы.

2. Циркуляция сил давления относительно единицы массы.

3. Циркуляция внутренних сил.

Остановимся подробнее на каждом из механизмов.

1. Влияние сил Кориолиса. Если вектор  направлен на нас и скорость  направлена вне контура , то скорость отклоняется вправо, циркуляция  изменяется по часовой стрелке, т.е. отрицательна, и следовательно, 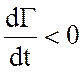 ( уменьшается). Таким образом, движение в поле абсолютного вихря меняет относительную завихренность.

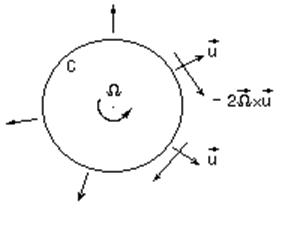
Рис. 3.3.

Это важно для крупномасштабных движений, когда границы циклонов или антициклонов заключают в себе большое количество вихревых нитей. В этом случае относительная завихренность практически всегда ненулевая.

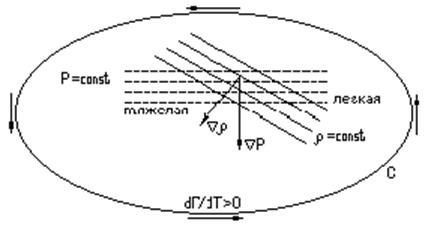
Рис. 3.4.

2. Циркуляция сил давления иллюстрируется следующим образом. По теореме Стокса.

.

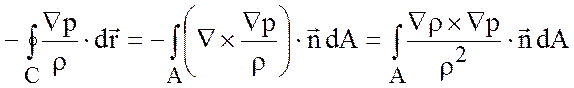Когда поверхности равной плотности и равного давления не совпадают (такое состояние жидкости называется бароклинным), тогда вектор бароклинности . На поверхности  на легкую и тяжелую жидкость действует одна и та же сила давления . Под действием этой силы легкая жидкость будет подниматься быстрее, чем тяжелая, и возникает циркуляция против часовой стрелки вокруг контура . Возникающая циркуляция стремится совместить поверхности равной плотности и давления. Этого не происходит, если . Действительно,

.

3. Не вдаваясь в анализ влияния массовых сил  на циркуляцию констатируем, что  ньютоновская вязкость уменьшает интенсивность вихревых трубок.

3.3. Теорема Кельвина.

Согласно определению имеем , где  - сечение трубки, перпендикулярное . Имеет место также соотношение, основанное на геометрических соображениях

.

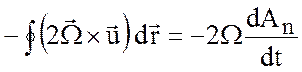Отсюда

.

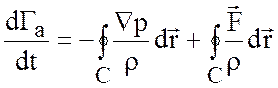Теорема Кельвина. Если

1. жидкость баротропна, ;

2. силы трения отсутствуют, ,

то абсолютная циркуляция сохраняется при движении, то есть

.

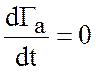Таким образом, если справедлива теорема Кельвина, то вихревая трубка движется вместе с жидкостью. Но так как  представляет собой сумму планетарной и относительной завихренности, то уменьшение одной вызовет, соответственно, увеличение другой. Итак, теорема Кельвина показывает, что механизм завихренности обуславливает такое взаимное изменение планетарной и относительной завихренности, при котором интенсивность трубки сохраняется. То есть, если вихревая трубка при движении переместилась к экватору, то планетарный вихрь уменьшился, следовательно, должен возникнуть дополнительный относительный вихрь, сохраняющий баланс абсолютного вихря. Если сечение трубки уменьшается, то ее интенсивность, а значит, и вихрь , должны увеличиваться обратно пропорционально площади сечения трубки.