Предмет геофизической гидродинамики. Уравнения движения. Основные упрощающие приближения, страница 3

2. Уравнения геофизической гидродинамики.

2.1. Уравнения в инерциальной  системе координат.

В основе геофизической гидродинамики лежит предположение о применимости уравнений непрерывной жидкости. Ограничимся эйлеровым описанием движения, при котором динамические переменные рассматриваются как функции вектора положения  и времени . При описании движения будем использовать такие динамические переменные, как  вектор скорости , давление , плотность , а также термодинамические переменные: температуру , внутреннюю энергию на единицу массы , удельную энтропию .

В этом разделе сформулируем уравнения движения в невращающейся, или инерциальной, системе отсчета, когда наблюдатель находится вне вращающегося тела, на котором находится жидкость.

Пусть на некоторый произвольный объем жидкости , ограниченный поверхностью , действует давление , тогда по формуле Гаусса-Остроградского полная сила, действующая на объем,

,

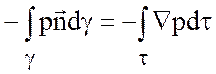где  - единичный вектор внешней нормали, 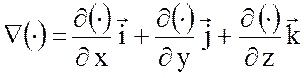- оператор градиента. По второму закону Ньютона

,

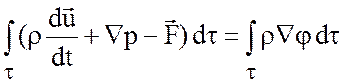где  - внутренняя сила (молекулярная вязкость),  - потенциал, которым описываются внешние силы, (например, сила тяжести, приливные потенциалы), а  - полная (индивидуальная) производная скорости , определяемая ускорение частицы формулой

,

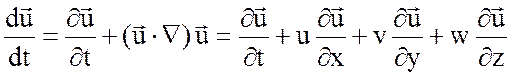Тогда, учитывая произвольность объема , получаем дифференциальный закон движения

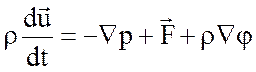.                                             (2.1)

Для ньютоновских жидкостей таких, как вода и воздух, , где - оператор Лапласа,  -  коэффициент внутренней молекулярной вязкости.

Если в жидкой среде отсутствуют источники или стоки массы, то закон сохранения массы для жидкого объема  имеет вид

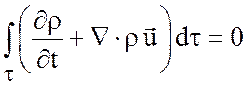
В дифференциальном виде закон сохранения массы записывается в виде уравнения неразрывности

,

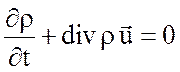которое можно переписать в виде

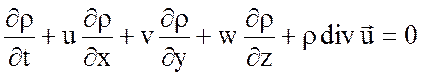
или

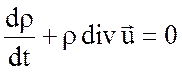                                                        (2.2)

В случае присутствия тепловых процессов уравнения для импульсов и уравнение неразрывности представляют собой незамкнутую систему. Поэтому для замыкания системы дополнительно рассматривается первый закон термодинамики

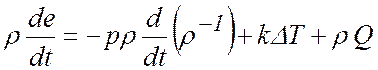,                                         (2.3)

где  - внутренняя энергия на единицу массы, - температура,  - скорость притока тепла от внешних источников на единицу массы,  - коэффициент теплопроводности, , величина 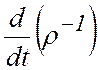 связана с изменением внутренней энергии системы в зависимости от изменений величины удельного объема. В уравнении (2.3) был отброшен член притока  тепла из-за вязкой диссипации, вследствие его малости для исследуемых процессов.

Далее введем термодинамическую функцию  - удельную энтропию, связанную с другими функциями состояния соотношением

.

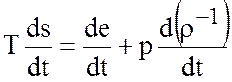В результате (2.3) можно переписать в виде

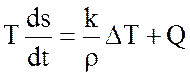.                                               (2.4)

Для замыкания системы уравнений необходимы дополнительные термодинамические соотношения - уравнения состояния

,

принимая во внимание которые, уравнение (2.4) можно переписать в форме

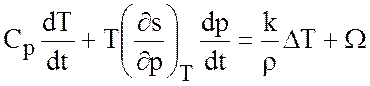,                                  (2.5)

где 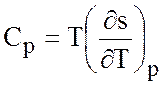 - удельная теплоемкость при постоянном давлении.

Далее, используем термодинамическое соотношение

,

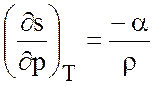где 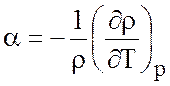 - коэффициент термического расширения. Тогда (2.5) перепишется в виде

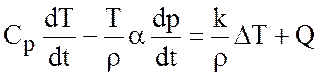.                                    (2.6)

Рассмотрим уравнения притока тепла в конкретных средах.

1. Атмосфера.

Уравнение состояния сухого воздуха хорошо описывается уравнением идеального газа 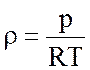, где  - газовая постоянная сухого воздуха. После подстановки удельной энтропии идеального газа  и коэффициента термического расширения   уравнение (2.6) принимает вид

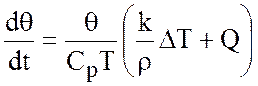,                                    (2.7)

где 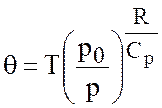 - потенциальная температура (температура, которую приобретала бы частица с температурой , адиабатически перенесенная из точки с давлением  в точку с давлением  - постоянное отсчетное давление. Приближенная формула для вычисления потенциальной температуры имеет вид

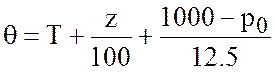
2. Океан.

Для воды, в которой эффекты сжимаемости незначительны, применимо простое уравнение состояния в приближении Буссинеска