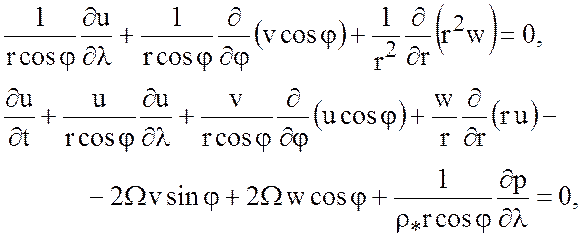
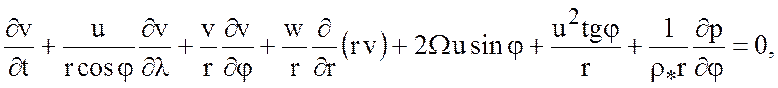 (4.5)
(4.5)
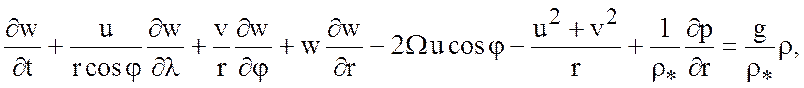
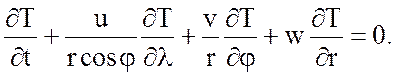
Вводим криволинейную систему координат
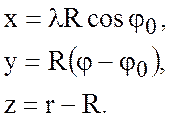
Начало координат соответствует точке ![]() , ось
, ось ![]() направлена
на восток, ось
направлена
на восток, ось ![]() - на север, ось
- на север, ось ![]() - вверх.
- вверх.
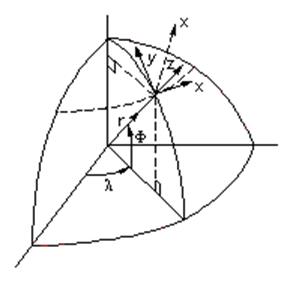
Рис. 4.1.
Тогда уравнение неразрывности перепишется в виде:
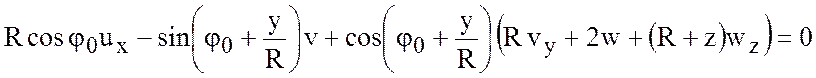 . (4.6)
. (4.6)
Введем безразмерные переменные
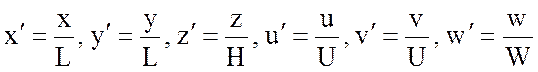 .
.
Здесь ![]() характерные
масштабы горизонтальной длины и скорости, а
характерные
масштабы горизонтальной длины и скорости, а ![]() и
и ![]() - соответственно, вертикального масштаба и
вертикальной скорости.
- соответственно, вертикального масштаба и
вертикальной скорости.
Будем далее считать, что все
величины ![]() и так далее имеют порядок единицы.
Модифицируем систему на примере уравнения неразрывности. Подставляя введенные
безразмерные величины в уравнение и опуская штрихи, получаем
и так далее имеют порядок единицы.
Модифицируем систему на примере уравнения неразрывности. Подставляя введенные
безразмерные величины в уравнение и опуская штрихи, получаем
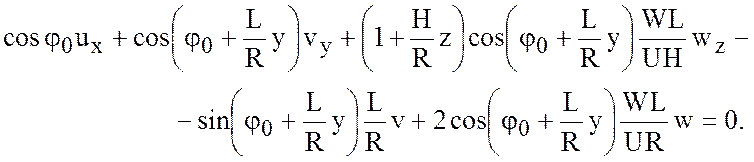 (4.7)
(4.7)
Пусть ![]() и
величина
и
величина 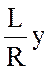 мала по сравнению с единицей. Это
выполняется, поскольку
мала по сравнению с единицей. Это
выполняется, поскольку ![]() ,
, ![]()
![]() ,
, ![]()
![]() . Следовательно, можно
разложить
. Следовательно, можно
разложить ![]() и
и ![]() в ряды
Тейлора в окрестности
в ряды
Тейлора в окрестности ![]() .
.
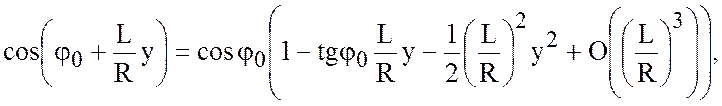
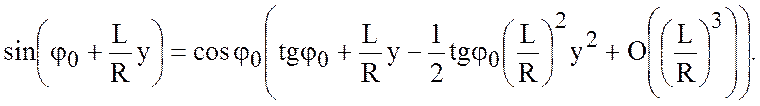
Далее, выбирая 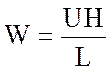 и
отбрасывая члены порядка
и
отбрасывая члены порядка 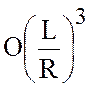 в (4.7), получим
в (4.7), получим
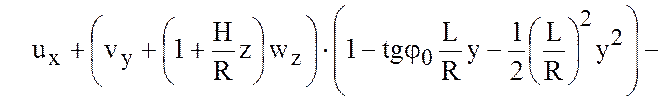
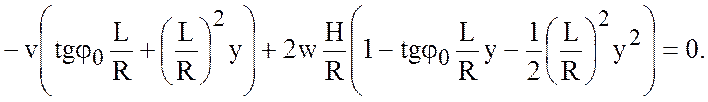
Полагаем, что
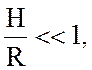
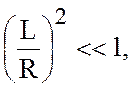 (4.8)
(4.8)
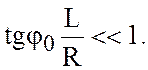
·
Первое условие (4.8)
означает, что рассматривается тонкий слой жидкости в пренебрежении радиальным
искажением ![]() .
.
·
Второе условие (4.8)
означает, что горизонтальный масштаб движения меньше радиуса Земли ![]() .
.
· Третье условие (4.8) означает, что приближение не работает в высоких широтах.
Тогда в результате для уравнения неразрывности получим соотношение
![]() . (4.9)
. (4.9)
Рассмотрим параметр Кориолиса. Заметим, что
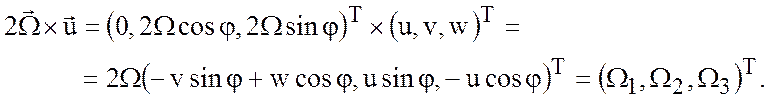
Тогда, проводя рассуждения и оценки
аналогичные предыдущим для первой компоненты ![]() , получим
выражение
, получим
выражение
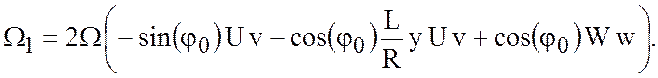
В размерном виде
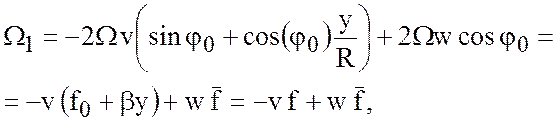
где ![]() -
параметр Кориолиса
-
параметр Кориолиса ![]() ,
, ![]() , а
, а ![]() . Остальные компоненты оцениваются
аналогично.
. Остальные компоненты оцениваются
аналогично.
С учетом сделанных предположений (4.8) можно показать, что нелинейные члены адвективной части ускорения в уравнениях движения сводятся к простому виду, совпадающему с формой в декартовой системе координат:
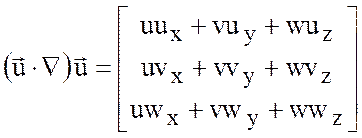 .
.
Следует отметить, что в вертикальной
составляющей адвективного ускорения отброшен член 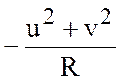 . Это
сделано из энергетических соображений после отбрасывания членов
. Это
сделано из энергетических соображений после отбрасывания членов ![]() ,
, ![]() в
адвективных членах для горизонтальных составляющих движения, компенсирующих это
слагаемое при выписывании соотношений для кинетической энергии системы.
Градиент давления также примет простой вид
в
адвективных членах для горизонтальных составляющих движения, компенсирующих это
слагаемое при выписывании соотношений для кинетической энергии системы.
Градиент давления также примет простой вид 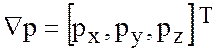 .
Окончательно, полная система уравнений при выполнении условий (4.8) примет вид
.
Окончательно, полная система уравнений при выполнении условий (4.8) примет вид
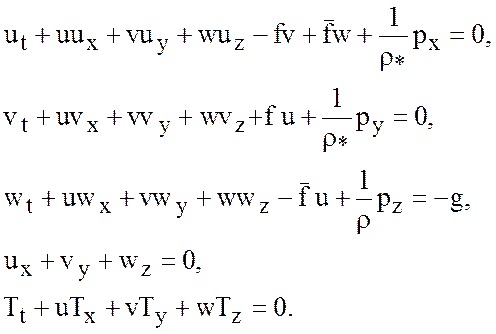 (4.10)
(4.10)
Таким образом, несмотря на введение
криволинейной системы координат, получили систему уравнений, близкую к системе
в декартовой системе координат. Система уравнений, содержащая параметр
Кориолиса с членом ![]() , называется приближением
, называется приближением ![]() -плоскости и переводит уравнения,
записанные на вращающейся сфере, в уравнения, записанные на вращающемся конусе,
касающемся сферы на широте
-плоскости и переводит уравнения,
записанные на вращающейся сфере, в уравнения, записанные на вращающемся конусе,
касающемся сферы на широте ![]() .
.
Если масштабы рассматриваемых
движений сравнимы с вертикальными масштабами, то можно использовать приближение
![]() -плоскости, когда
-плоскости, когда ![]() (вращающийся цилиндр). Итак, если
(вращающийся цилиндр). Итак, если
· ![]() , необходимо
рассматривать сферическую систему координат;
, необходимо
рассматривать сферическую систему координат;
· 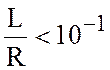 , можно использовать приближение
, можно использовать приближение ![]() -плоскости;
-плоскости;
· ![]() , можно использовать
приближение
, можно использовать
приближение ![]() -плоскости.
-плоскости.
4.3. Приближение квазистатики.
Продолжаем рассмотрение движений с большими масштабами. Если к условиям (4.8) дополнительно принять, что
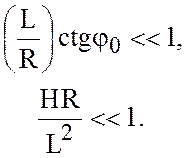 (4.11)
(4.11)
то слагаемыми ![]() в
уравнениях движения можно пренебречь. Первое условие (4.11) исключает
экваториальные зоны океана, второе - выделяет крупномасштабные движения. Если
теперь оценить все члены с вертикальными ускорениями, то они в принятых
условиях будут существенно меньше, чем гидростатические члены. В этом случае
применимо «квазигидростатическое» приближение, когда третье уравнение движения
приобретает вид
в
уравнениях движения можно пренебречь. Первое условие (4.11) исключает
экваториальные зоны океана, второе - выделяет крупномасштабные движения. Если
теперь оценить все члены с вертикальными ускорениями, то они в принятых
условиях будут существенно меньше, чем гидростатические члены. В этом случае
применимо «квазигидростатическое» приближение, когда третье уравнение движения
приобретает вид
![]() . (4.12)
. (4.12)
Остальные уравнения системы имеют вид
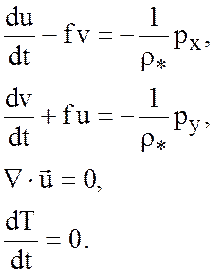 (4.13)
(4.13)
где
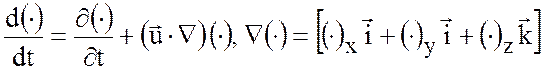 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.