Теория Дебая – Хюккеля позволяет рассчитывать коэффициенты активности ионов в растворах, содержащих другие ионы. Для наглядности представим себе большой многозарядный ион, например, положительно заряженную коллоидную частицу, которая помещается в раствор электролита. Вблизи этой частицы происходит перераспределение ионов, возникает избыток анионов и недостаток катионов в сравнении со средней по раствору концентрацией. Если зафиксировать это распределение, или ионную атмосферу, и убрать из раствора коллоидную частицу, то в месте, где она располагалась, обнаружится потенциал, создаваемый ионной атмосферой. Ясно, что если вернуть частицу обратно в раствор, то её энергия будет зависеть от электрического потенциала в точке, где она находится. Задача теории состоит в определении коэффициента активности (g) заряженной частицы, зависящего от энергии её взаимодействия с ионной атмосферой. Выводы теории оказываются справедливыми не только для коллоидных частиц, но и для частиц небольшого размера, включая однозарядные ионы.
Энергия взаимодействия иона со своей ионной атмосферой E равна разности химических потенциалов иона в реальном растворе (растворе с ионной силой I) и растворе с нулевой ионной силой (I = 0), который мы будем считать идеальным:
.
Напомним, что ионной силой раствора называется величина
,
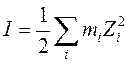где mi – моляльная концентрация иона сорта i, Zi – его заряд.
Важно заметить, что рассчитываемый таким образом коэффициент активности учитывает неидеальность раствора, связанную только с влиянием ионной силы.
Логика дальнейшего расчёта, который мы не будем приводить полностью, состоит в следующем.
Потенциал y на расстоянии r от иона (коллоидной частицы) с зарядом Z в среде с диэлектрической проницаемостью e и нулевой ионной силой равен
.
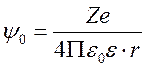Распределение других присутствующих в растворе катионов и анионов вокруг центрального иона в таком потенциале задаётся формулой Больцмана. Потенциал, создаваемый всеми зарядами на расстоянии r от иона, можно получить, решая уравнение Пуассона. Решение для раствора с ионной силой I (моль/м3) при некоторых упрощающих предположениях выглядит так:
.
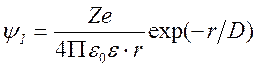Величина D называется радиусом ионной атмосферы и равна
.
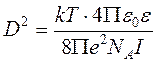Как и следовало ожидать, присутствие ионной атмосферы
приводит к тому, что потенциал вокруг центрального иона падает более быстро,
чем при нулевой ионной силе, поскольку заряд центрального иона частично
экранируется. При I 
0 радиус ионной атмосферы стремится к
бесконечности, экспонента стремится к единице, а yI стремится к y0.
Ясно, что потенциал y а, создаваемый только ионной атмосферой без учёта вклада центрального иона, можно найти как разность величин y I и y 0.
.
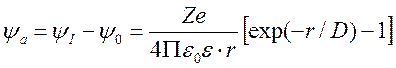Предполагая,
что показатель экспоненты << 1, находим потенциал ионной атмосферы в
месте расположения центрального иона при r
0.
.
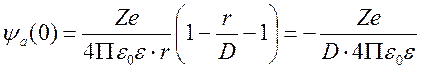Энергия взаимодействия центрального иона Ze со своей ионной атмосферой в расчёте на 1 моль равна
.
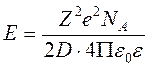Искомый коэффициент активности находится как
,
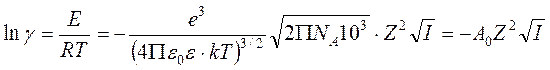где k = 1,3810-23 Дж/К – постоянная Больцмана, e = 1,610-19 кулон – заряд электрона, численный коэффициент 103 вводится, чтобы ионную силу можно было подставлять в моль/л.
В системе CGSE эта формула выглядит так:
,
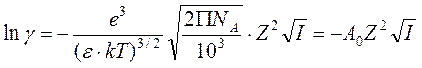где k = 1,3810-16 эрг/К, e = 4,810-10 единиц заряда электрона в системе CGSE. В таком виде она часто фигурирует в литературе.
Если вместо натурального логарифма использовать десятичный, а ионную силу подставлять в моль/л, то для воды при 25 0С величина A0 равна 0,509:
.
Эта формула известна как первое приближение теории Дебая –Хюккеля для коэффициента активности иона в растворе электролита. Для водных растворов 1,1-электролитов она справедлива до концентраций электролита порядка 10-2 М. Второе приближение учитывает конечный размер центрального иона и приводит к следующей формуле:
.
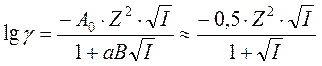В знаменателе перед корнем стоит размерный коэффициент (aB), a – диаметр иона, В – константа, зависящая от произведения eT. Как видно из таблицы, для ионов диаметром 0,3 нм, находящихся в водном растворе, коэффициент (аВ) примерно равен единице.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.