Практикум по физической химии. Потенциометрия: Методическое пособие, страница 3

.

Если Т и Р постоянны, то изменение свободной энергии Гиббса при протекании реакции равно полезной работе, которая есть максимальная полезная работа, если процесс проводится обратимо:

.                                            (2)

Сопоставляя выражения (1) и (2), получаем следующее соотношение:

,                                         (3)

где Е – разность электродных потенциалов.

Соотношение (3) очень важно, так как даёт простую связь между легко измеряемой величиной E и изменением энергии Гиббса в ходе реакции. Рассмотрим, элемент Даниэльса – Якоби, в котором протекает реакция

.                              (I)

Измеряя разность потенциалов E между цинковой и медной пластинками этого элемента, мы легко получаем величину . Столь же легко могут быть найдены и многие другие термодинамические характеристики реакции. Например, дифференцируя соотношение (3) по температуре, получаем выражение для изменения энтропии в ходе реакции:

.

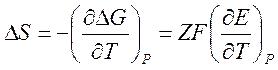Следовательно, измерение температурного коэффициента разности электродных потенциалов гальванического элемента фактически эквивалентно измерению изменения энтропии при протекании в нём химической реакции.

Уравнение изотермы химической реакции применительно к процессу (I) выглядит следующим образом:

,

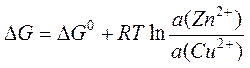где a(Zn²⁺) и a(Cu²⁺) – активности (концентрации) соответствующих ионов в растворах, а – стандартная энергия Гиббса. Если разделить обе части этого уравнения на (–Z×F) и учесть соотношение (3), получим следующее равенство:

,                                 

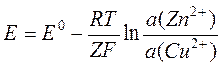где Z – число электронов, переносимое при протекании одного акта реакции (I), а E⁰ (= 0,916 В) – разность стандартных электродных потенциалов. Это уравнение Нернста, написанное для процесса в элементе Даниэльса – Якоби.

В общем случае уравнение Нернста может быть записано, как

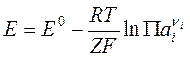,                                   (4)

где  – произведение реакции, а Е⁰ – стандартная разность электродных потенциалов гальванического элемента, т. е. значение, которое принимает величина Е, если активности ионов и летучести газов, входящие в уравнение Нернста, равны единице. Величина     E⁰ связана с константой равновесия токообразующей реакции соотношением

.

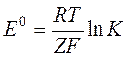Иногда при написании уравнения Нернста в произведение реакции включают «активности конденсированных фаз», а затем полагают их равными единице. Такой приём полезен как мнемоническое правило.

Уравнение Нернста можно применить не только к гальваническому элементу в целом, но и к составляющим его электродам. Следует учитывать, что электродные реакции принято записывать в справочниках как реакции восстановления. Поэтому цинковому электроду (электроду Zn²⁺|Zn) отвечает электродная реакция

Zn²⁺ + 2e^– ® Zn,

 а медному электроду (электроду Cu²⁺|Cu) – электродная реакция

Cu²⁺ + 2e^– ® Cu.

Уравнение Нернста для цинкового и медного электродов может быть записано соответственно как

,

.

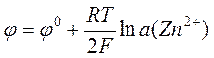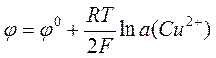Для железоионного электрода Pt½Fe³⁺,Fe²⁺  

.

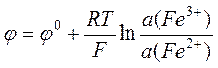В общем случае уравнение Нернста для полуэлемента (электрода) может быть записано, как

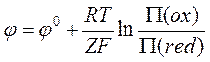,                                (5)

где  и  – произведения активностей окисленных и восстановленных форм соответственно.

       Как известно, для самопроизвольно протекающего процесса при P, Т = const выполняется условие . Поэтому в силу соотношения (3) реакция в гальваническом элементе будет самопроизвольно протекать слева направо, если Е > 0. Для того чтобы знак разности электродных потенциалов элемента имел положительное значение, используют следующие правила:

– При символической записи гальванического элемента его изображают таким образом, что на левом электроде идёт процесс окисления, т. е. он является анодом, а на правом электроде идёт восстановление, т. е. он является катодом. Например, в элементе Даниэльса – Якоби процесс на левом электроде Zn®Zn²⁺ + 2e^–,      а на правом электроде Cu²⁺ + 2e^–®Cu. Данный элемент изображается как Zn|Zn²⁺||Cu²⁺|Cu. При этом одинарная вертикальная черта означает границу раздела фаз, двойная черта – солевой мостик; вещества, находящиеся в одной фазе, пишутся через запятую.