Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції

Розділ 5

Апроксимація функцій

Апроксимація  (від лат. approximo - наближаюся) - заміна одних математичних об'єктів іншими, якомось чином близькими до вихідних. Апроксимація дозволяє досліджувати числові характеристики і якісні властивості об'єкта, зводячи задачу до вивчення більш простих або більш зручних об'єктів (наприклад таких, характеристики яких легко обчислюються або властивості яких уже відомі). У теорії чисел вивчаються діофантові наближення, зокрема наближення ірраціональних чисел раціональними. У геометрії і топології розглядаються апроксимації кривих, поверхонь, просторів і відображень. Деякі розділи математики цілком присвячені апроксимації, наприклад наближення функцій.

5.1 Поняття про наближення функцій

Нехай величина у є функцією аргумента х. Це означає, що будь-якому значенню х з області визначення поставлено у відповідність значення у. Разом з тим на практиці часто невідомий явний зв'язок між у та х, тобто неможливо записати цей зв'язок у вигляді деякої залежності y=f(x). У деяких випадках навіть при відомій залежності y=f(x) вона настільки громіздка (наприклад, містить вирази, що важко обчислюються, складні інтеграли і т.п.), що її використовувати в практичних розрахунках важко.

Найбільш поширеним і практично важливим випадком, коли вигляд зв'язку між параметрами х та у невідомий, є його завдання у вигляді деякої таблиці {x_i, y_i}. Це означає, що дискретній множині значень аргумента {x_i} поставлена у відповідність множина значень функції {y_i} (i=0,1,…,n). Ці значення - або результати розрахунків, або експериментальні дані. На практиці нам можуть знадобитися значення величини у і в інших точках поза вузлами x_i. Однак одержати ці значення можна лише шляхом дуже складних розрахунків або проведенням дорогих експериментів.

Таким чином, з огляду економії часу і засобів ми приходимо до необхідності використання наявних табличних даних для наближеного обчислення невідомого параметра у при будь-якому значенні (з деякої області) визначального параметра х, оскільки точний зв'язок y = f(x) -  невідомий.

Цій меті підпорядкована задача про наближення (апроксимацію) функцій: задану функцію f(x) потрібно приблизно замінити (апроксимувати) деякою функцією F(x) так, щоб відхилення (у деякому змісті) F(x) від f(x) у заданій області було найменшим. Функція F(x) при цьому називається апроксимуючою.

Апроксимуючими функціями можуть бути поліноміальні, тригонометричні, експонентні та ін.

Якщо наближення будується на заданій дискретній множині точок {x_i}, то апроксимація називається точковою. До неї належать інтерполяція, середньоквадратичне наближення та ін. При побудові наближення на неперервній множині точок (наприклад, на відрізку [a,b]) апроксимація називається неперервною (або інтегральною).

Одним із основних типів точкової апроксимації є інтерполяція. У цьому випадку апроксимуюча функція проходить через задані вузлові точки. Іноді наближення табличних даних методом інтерполяції проводити незручно. Так, наприклад, якщо дані в таблиці неточні, то збіг значень інтерполяційної функції у вузлах з табличними даними означає, що вона точно повторює помилки таблиці. У таких випадках використовують інші види апроксимації, наприклад, метод найменших квадратів. Цим методом апроксимуюча функція будується так, щоб сума квадратів відстаней від ординат точок до лінії графіка апроксимуючої функції для однакових абсцис була найменшою.

5.2 Iнтерполювання функції

  Загальна постановка задачі інтерполювання така. Задані значення  функції аргумента  при відповідних його значеннях  . Побудувати неперервну функцію , що належить до заданого класу функцій, таку, що вона збігається з  при значеннях аргумента  . Така функція називається інтерполюючою. Точки x_i, i=1,…,n називаються вузлами інтерполяції і вони утворюють сітку розбиття , а y_i - вузловими значеннями.

  У такому формулюванні розв'язок задачі є невизначеним, бо крізь задані точки можна провести безліч кривих. Тому загальну постановку дещо звужують, задаючи не тільки клас інтерполюючої функції, але й додаткову умову мінімальної її складності.

  Наприклад, для найбільш поширеного поліноміального інтерполювання (при якому інтерполююча функція обирається серед поліномів аргумента ), додатковою умовою є мінімальний порядок інтерполюючого полінома. З цього випливає, що якщо первісну функцію задано лише двома точками, її треба інтерполювати поліномом першого порядку (через дві задані точки проходить єдина пряма), якщо трьома - параболою другого порядку і так далі. Взагалі функція, задана своїми  значеннями (у  точках), інтерполюється однозначно поліномом -го порядку, тобто таким

.    (5.1)

Тепер задача інтерполювання звелася до пошуку значень  невідомих коефіцієнтів полінома (5.1) з умови набуття ним значень  при значеннях аргумента .

  Існують кілька способів визначення цих коефіцієнтів. Вони відрізняються методикою обчислень, зручною в одних і незручною в інших випадках. Але при ідеальних обчисленнях вони, природно, призводять до тих самих результатів, тобто до того самого полінома.

5.2.1 Інтерполювання за Лагранжем

За цією методикою попередньо визначають допоміжні поліноми -го порядку  такі, що

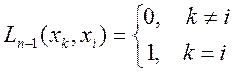.                     (5.2)