Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 4

                         (5.23)

Доведено, що серед усіх можливих  значень  на відрізку  корені  многочлена  мають ту чудову властивість, що для них величина

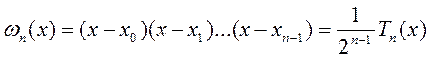(5.24)

має найменше за модулем максимальне значення.

Беручи до уваги (5.24), запишемо

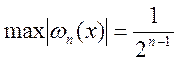.                      (5.25)

Виходячи з властивостей коренів многочленів Чебишева першого роду і визначення інтерполяційного многочлена  -го степеня на відрізку  можна стверджувати, що якщо за  вузлів інтерполювання взяти корені многочлена  то максимальне значення похибки на цьому відрізку буде найменшим для всіх можливих варіантів вибору  вузлів інтерполювання. Інтерполяційний многочлен, наділений такою властивістю, називається многочленом найкращого наближення. Оцінка (5.19) при цьому набирає вигляду

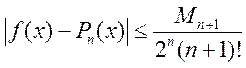, де .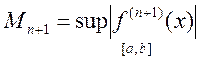

Якщо інтерполювання проводиться на довільному відрізку , то заміною змінної

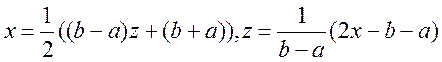
цей відрізок можна звести до відрізка  При цьому корені многочлена  будуть знаходитися в точках

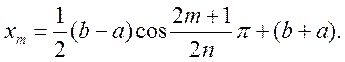
Оцінка похибки має вигляд

.

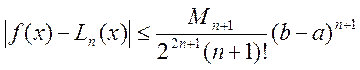5.2.5 Збіжність процесу інтерполяції

Розглянемо послідовність сіток

w_n: a=x₀<x₁<…<x_n-1 <x_n=b.

Кажуть, що інтерполяційний поліном  рівномірно збігається до заданої функції , якщо при max (x -x_n-1) ® 0   . Справедливі такі теореми.

Теорема Фабера. Для будь-якої послідовності сіток w_n знайдеться  така, що збіжність відсутня.

Теорема Марцинкевича. Для будь-якої функції знайдеться послідовність сіток

Приклад. Використовуючи інтерполяційний поліном Ньютона, визначити f(0.14), де y=f(x) задана таблично.

Розв’язання. Складаємо таблицю скінченних різниць, користуючись пакетом Excel:

	A	B	C	D	E	F	G
1	x	y
2	0	0	=B3-B2	=C3-C2	=D3-D2	=E3-E2	=F3-F2
3	0,1	0,1002	=B4-B3	=C4-C3	=D4-D3	=E4-E3
4	0,2	0,2013	=B5-B4	=C5-C4	=D5-D4
5	0,3	0,3045	=B6-B5	=C6-C5
6	0,4	0,4108	=B7-B6
7	0,5	0,5211

У результаті отримаємо таке:

	A	B	C	D	E	F	G
1	x	y
2	0	0	0,1002	0,0009	0,0012	-0,0002	0,0001
3	0,1	0,1002	0,1011	0,0021	0,0010	-0,0001
4	0,2	0,2013	0,1032	0,0031	0,0009
5	0,3	0,3045	0,1063	0,0040
6	0,4	0,4108	0,1103
7	0,5	0,5211

Для розрахунку f(0.14) скористаємося інтерполяційним поліномом Ньютона, покладаючи, що x₀=0.1 та h=0.1; тоді q=(x-x₀)/h=(0,14-0,1)/0,1=0,4. Звідси за формулою визначаємо:

f(0.14)≈0,1002+0,1011*0,4+0,0021*0,4*(-0,6)/2+ +0,1010*0,4*(-0,6)*(-1,6)/6 ≈ 0,1405, або у MS Excel у даному випадку, формула матиме такий вигляд: =B3+Q*C3+Q*(Q-1)*D3/ФАКТР(2)+Q*(Q-1)*(Q-2)*

*E3/ФАКТР(3), де Q - адреса комірки із розрахованим значенням q.